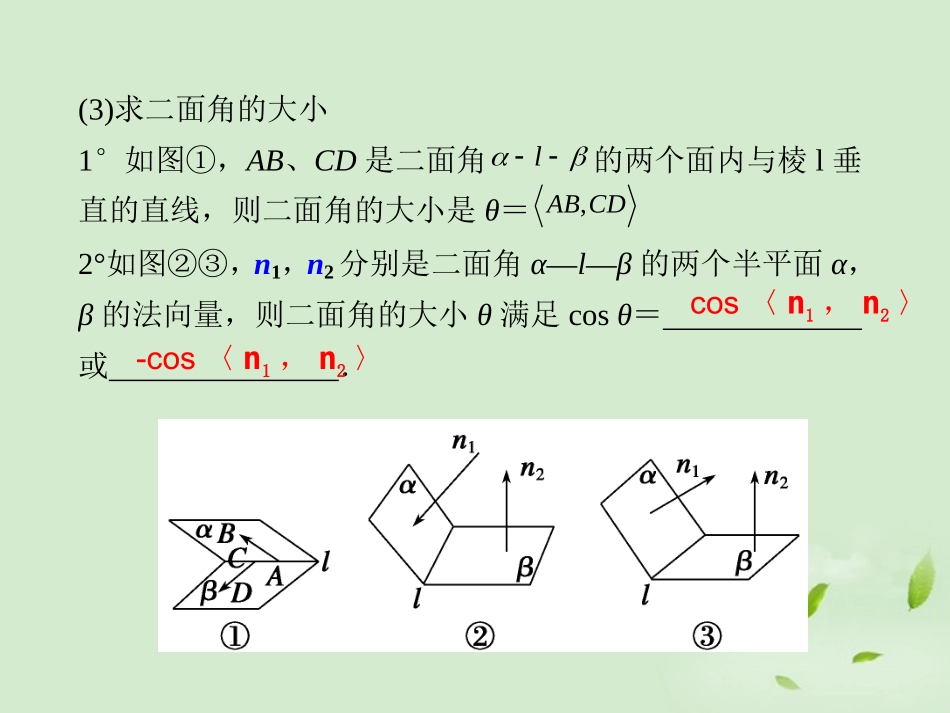
§8.8立体几何中的向量方法(Ⅱ)——求空间角与距离基础知识自主学习要点梳理1.直线的方向向量与平面的法向量的确定(1)直线的方向向量:在直线上任取一非零向量作为它的方向向量.(2)平面的法向量可利用方程组求出:设a,b是平面α内两不共线向量,n为平面α的法向量,则求法向量的方程组为n·a=0n·b=0.2.空间向量与空间角的关系(1)设异面直线l1,l2的方向向量分别为m1,m2,则l1与l2所成的角θ满足cosθ=|cos〈m1,m2〉|.(2)设直线l的方向向量和平面α的法向量分别为m,n,则直线l与平面α所成角θ满足sinθ=|cos〈m,n〉|.(3)求二面角的大小1°如图①,AB、CD是二面角l的两个面内与棱l垂直的直线,则二面角的大小是θ=,ABCD�2°如图②③,n1,n2分别是二面角α—l—β的两个半平面α,β的法向量,则二面角的大小θ满足cosθ=或.cos〈n1,n2〉-cos〈n1,n2〉3.点面距的求法如图,设AB为平面的一条斜线段,n为平面的法向量,则B到平面的距离d=AB�nn[难点正本疑点清源]1.空间各种角的计算方法都是转化为平面角或两向量的夹角来计算的,对空间各种角概念必须深刻理解.平行和垂直可以看作是空间角的特殊情况.2.向量法通过空间坐标系把空间图形的性质代数化,避免了寻找平面角和垂线段等诸多麻烦,使空间点线面的位置关系的判定和计算程序化、简单化.主要是建系、设点、计算向量的坐标、利用数量积的夹角公式计算.3.求点到平面距离的方法:①垂面法:借助面面垂直的性质来作垂线,其中过已知点确定已知面的垂面是关键;②等体积法,转化为求三棱锥的高;③等价转移法;④法向量法.基础自测1.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a=(1,0,1),b=(0,1,1),那么,这条斜线与平面所成的角是()A.90°B.30°C.45°D.60°解析 cos〈a,b〉=12·2=12,又 〈a,b〉∈[0°,180°],∴〈a,b〉=60°.D2.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角的大小为()A.45°B.135°C.45°或135°D.90°解析cos〈m,n〉=m·n|m||n|=11×2=22,即〈m,n〉=45°,其补角为135°,∴两平面所成的二面角为45°或135°.C3.已知向量m,n分别是直线l和平面α的方向向量、法向量,若cos〈m,n〉=-12,则l与α所成的角为()A.30°B.60°C.120°D.150°解析设l与α所成的角为θ,则sinθ=|cos〈m,n〉|=12,∴θ=30°.A4.如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO—A′B′C′D′,A′C的中点E与AB的中点F的距离为________.解析由图易知A(a,0,0),B(a,a,0),C(0,a,0),A′(a,0,a).∴Fa,a2,0,Ea2,a2,a2.∴|EF|=a-a22+a2-a22+0-a22=a24+a24=22a.22a5.如图所示,在三棱柱ABC—A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是________.解析以BC为x轴,BA为y轴,BB1为z轴,建立空间直角坐标系.设AB=BC=AA1=2,则C1(2,0,2),E(0,1,0),F(0,0,1),则EF�=(0,-1,1),1BC�=(2,0,2),∴EF�1BC�=2,∴cos1,EFBC�=22×22=12,∴EF和BC1所成角为60°.答案60°题型分类深度剖析题型一求异面直线所成的角例1如图所示,在长方体ABCD—A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=BF=1.求直线EC1与FD1所成的角的余弦值.思维启迪:(1)本题易于建立空间直角坐标系,把EC1与FD1所成的角看向量EC1→与FD1→的夹角,用向量法求解.(2)平移线段C1E让C1与D1重合,转化为平面角,放到三角形中,用几何法求解.解方法一以A为原点,1ABADAA�、、分别为x轴、y轴、z轴的正向建立空间直角坐标系,则有D1(0,3,2),E(3,0,0),F(4,1,0),C1(4,3,2),于是EC1→=(1,3,2),FD1→=(-4,2,2),设EC1与FD1所成的角为β,则:cosβ=1111ECFDECFD��=1×-4+3×2+2×212+32+22×-42+22+22=2114,∴直线EC1与FD1所成的角的余弦值为2114.方法二延长BA至点E1,使AE1=1,连接E1F、DE1、...