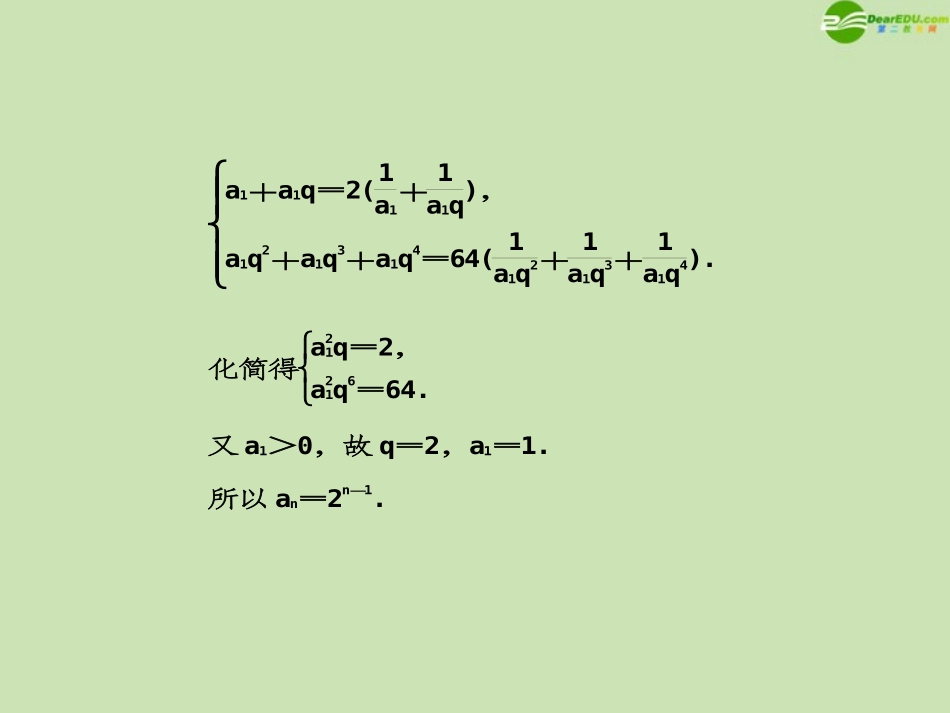高考数学一轮复习 数列求和调研课件 文 新人教A版 课件VIP免费

专题研究数列求和例1(2010·全国卷Ⅱ，文)已知{an}是各项均为正数的等比数列，且a1＋a2＝2(1a1＋1a2)，a3＋a4＋a5＝64(1a3＋1a4＋1a5)．(1)求{an}的通项公式；(2)设bn＝(an＋1an)2，求数列{bn}的前n项和Tn.【解析】(1)设公比为q，则an＝a1qn－1.由已知有专题讲解题型一通项分解法a1＋a1q＝2(1a1＋1a1q)，a1q2＋a1q3＋a1q4＝64(1a1q2＋1a1q3＋1a1q4).化简得a21q＝2，a21q6＝64.又a1＞0，故q＝2，a1＝1.所以an＝2n－1.(2)由(1)知bn＝(an＋1an)2＝a2n＋1a2n＋2＝4n－1＋14n－1＋2.因此Tn＝(1＋4＋…＋4n－1)＋(1＋14＋…＋14n－1)＋2n＝4n－14－1＋1－14n1－14＋2n＝13(4n－41－n)＋2n＋1.探究1将数列中的每一项拆成几项，然后重新分组，将一般数列求和问题转化为特殊数列的求和问题，我们将这种方法称为通项分解法，运用这种方法的关键是通项变形．思考题1求数列0.9,0.99,0.999，…，0.前n项的和Sn.【答案】n－19(1－0.1n)题型二倒序相加法例2设数列{an}为等差数列，试证Sn＝n（a1＋an）2.【思路分析】可用倒序相加法，证明从略．探究2如果一个数列{an}，与首末两项等距离的两项之和等于首末两项之和，可采用把正着写与倒着写的两个和式相加，就得到一个常数列的和，这一求和方法称为倒序相加法．思考题2设f(x)＝12x＋2，利用课本中推导等差数列前n项和的公式的方法，可求得f(－5)＋f(－4)＋…＋f(0)＋…＋f(5)＋f(6)的值为________．∴f(－5)，f(－4)，…，f(5)，f(6)共有11＋1＝12项．由f(－5)、f(6)；f(－4)、f(5)；…；f(0)、f(1)共有6对，且该数列为等差数列．∵【答案】6＋(－5)＝1，又f(0)＋f(1)＝11＋2＋12＋2＝11＋2＋121＋2＝2＋121＋2＝12＝22∴f(－5)＋f(－4)＋…＋f(6)＝6·22＝32.例3求和：(1)Sn＝11×2＋12×3…＋1nn＋1(2)Sn＝11×3＋12×4＋…＋1nn＋2【解析】(1)Sn＝1－12＋12－13＋…＋1n－1n＋1题型三裂项相消法＝1－1n＋1＝nn＋1(2)Sn＝121－13＋12－14＋…＋1n－1n＋2＝121＋12－1n＋1－1n＋2探究3裂项相消法求和就是将数列中的每一项拆成两项或多项，使这些拆开的项出现有规律的相互抵消，看有几项没有抵消掉，从而达到求和的目的．思考题3已知直线(3m＋1)x＋(1－m)y－4＝0所过定点的横、纵坐标分别是等差数列{an}的第一项与第二项，若bn＝1an·an＋1，数列{bn}的前n项和为Tn，则T10＝()A.921B.1021C.1121D.2021【解析】依题意，将(3m＋1)x＋(1－m)y－4＝0化为(x＋y－4)＋m(3x－y)＝0，令x＋y－4＝03x－y＝0，解得x＝1y＝3，所以直线(3m＋1)x＋(1－m)y－4＝0过定点(1,3)，所以a1＝1，a2＝3，公差d＝2，an＝2n－1，bn＝1an·an＋1＝12(12n－1－12n＋1)，T10＝12×(11－13＋13－15＋…＋120－1－120＋1)＝12×(11－121)＝1021.故选B.【答案】B题型四错位相减法例4求和：Sn＝1×12＋3×14＋5×18＋…＋2n－12n.【思路分析】数列1,3,5，…，2n－1成等差数列，数列12，14，18，…，12n组成等比数列，此例利用错位相减法可达目的．【解析】∵Sn＝1×12＋3×14＋5×18＋…＋(2n－1)×12n，①∴12Sn＝1×14＋3×18＋…＋(2n－3)×12n＋(2n－1)×12n＋1.②①－②，得Sn＝1×12＋2×14＋2×18＋…＋2×12n－(2n－1)×12n＋1＝1×12＋2×14－2×12n＋11－12－(2n－1)×12n＋1＝32－2n＋32n＋1.∴Sn＝3－2n＋32n(n∈N*)．探究4①如果一个数列的各项是由一个等差数列与一个等比数列对应项乘积组成，此时求和可采用错位相减法．②运用错位相减法求和，一般和式比较复杂，运算量较大，易会不易对，应特别细心，解题时若含参数，要注意分类讨论．思考题4设正项等比数列{an}的首项a1＝12，前n项和为Sn，且210S30－(210＋1)S20＋S10＝0，(1)求{an}的通项；(2)求{nSn}的前n项和Tn.【解析】(1)an＝12n，n＝1,2，…(2)∵{an}是首项a1＝12，公比q＝12的等比数列，∴Sn＝12(1－12n)1－12＝1－12n，nSn＝n－n2n.则数列{nSn}的前n项和Tn＝(1＋2＋…＋n)－(12＋222＋…＋n2n)①Tn2＝12(1＋2＋…＋n)－(122＋223＋…＋n－12n＋n2n＋1)②①－②，得Tn2＝12(1＋2＋…＋n)－(12＋122＋…＋12n)＋n2n＋1＝n(n＋1)4－12(1－12n)1－12＋n2n＋1，即Tn＝n(n＋1)2＋12n－1＋n2n－2.专题训练（专题训练（11））