高中数学：正弦函数性质课件新课标人教B版必修4 课件VIP免费

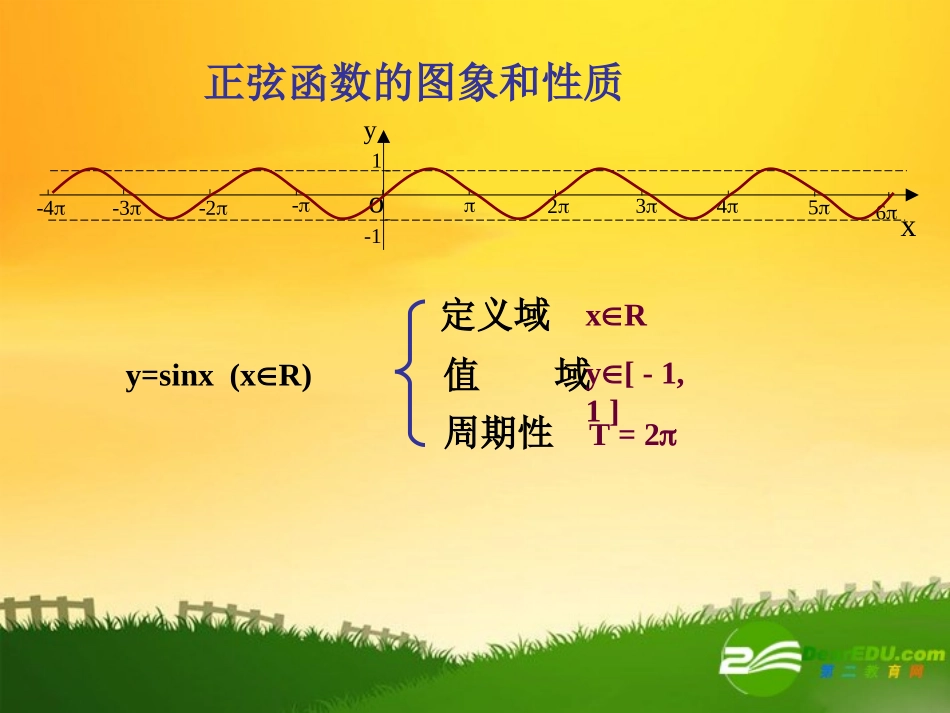
正弦函数的性质一、作出正弦函数y=sinx的图像0232二、两段有用的图像222302正弦函数的图象和性质x6yo--12345-2-3-41y=sinx(xR)定义域值域周期性xRy[-1,1]T=2sin(-x)=-sinx(xR)y=sinx(xR)x6yo--12345-2-3-41是奇函数定义域关于原点对称正弦函数的奇偶性正弦函数的单调性y=sinx(xR)增区间为[，]其值从-1增至122xyo--1234-2-31223252722325xsinx2223…0………-1010-1减区间为[，]其值从1减至-1223[+2k,+2k],kZ22[+2k,+2k],kZ223三、观察上面图像，指出正弦函数的性质定义域R值域[-1,1]奇偶性奇周期性单调性max&min2:2T最小正周期＝k减＋当增当]232,22[]22,22[kkxkkx1y1minmax－y).32sin(32.3sin12xyxy求下列函数的周期例.sin111的定义域求函数例xy例3(1)求函数在x取何值时到达最大值？在x取何值是到达最小值？)62sin()(xxf关键点：把看作一个整体。62.)18sin()10sin(,4的大小与比较不求值例(2)求函数在x取何值时到达最大值？在x取何值是到达最小值？2(sin1)2yx四、正弦函数性质的简单应用____)326(sinxy2的值域是、函数x3、函数的定义域是______xysin2114、函数______sin1的定义域是xy,2sin5?.xyx1当取什么值时函数取最大值和最小值并求出它的最大值和最小值