高中数学 121(任意角的三角函数2)课件 苏教版必修4 课件VIP免费

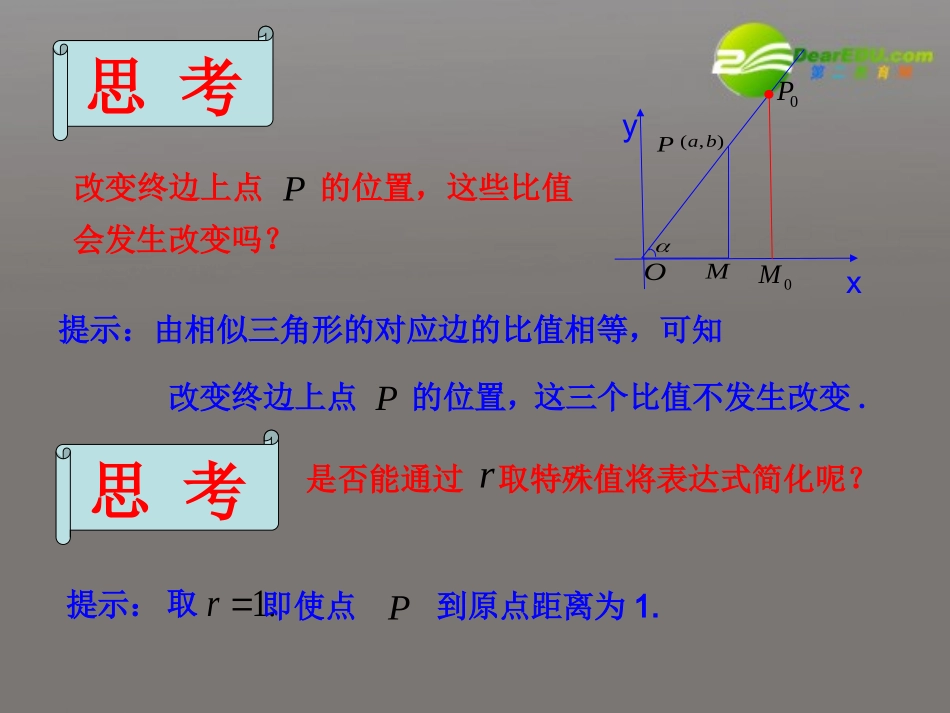
abrOMP1.2任意角的三角函数1.（回忆）锐角三角函数（直角三角形中）abrarbtancossin2.锐角三角函数（直角坐标系中）使锐角的顶点与原点重合，始边与轴的正半轴重合.xabrarbtancossinxy),(baabrOMP的终边上任取一点它与原点的距离),(bap022bar，.在OMPxy),(ba0M0P.思考改变终边上点的位置，这些比值P会发生改变吗？这三个比值不发生改变.改变终边上点的位置，P提示：由相似三角形的对应边的比值相等，可知思考是否能通过r取特殊值将表达式简化呢？提示：.1r取即使点到原点距离为1.PabOMMPaOPOMbOPMPtancossin以原点O为圆心，以单位长度为半径的圆，称为单位圆.3.锐角三角函数（在单位圆中）那么这样的点的轨迹是什么呢？MyoP),(bax14.用单位圆定义任意角的三角函数)0,1(AxyoP),(yx的终边设是一个任意角，它的终边与单位圆交于一点),(yxp，那么（１）ysinxy叫做的正切，记作tan，即（３）)0(tanxxy（２）xcosx叫做cos，即的余弦，记作y叫做的正弦，记作sin，即正弦、余弦、正切都是以角为自变量，以单位圆上的点的坐或坐标的比值为函数值的函数，我们将它们统称为三角函数.标)0,1(AxyoP),(yx的终边说明（1）正弦就是交点的纵坐标，余弦就是交点横坐标的比值.的横坐标，正切就是交点的纵坐标与（3）由于角的集合与实数集之间可以建立一一对应关系，三角函数可以看成是自变量为实数的函数..（2）正弦、余弦总有意义.当的终边在y横坐标等于0，xytan无意义，此时)(2zkk轴上时，点P的直角三角形中定义锐角三角函数abrarbtan,cos,sin直角坐标系中定义锐角三角函数abrarbtan,cos,sin单位圆中定义锐角三角函数ababtan,cos,sin单位圆中定义任意角的三角函数,sinyxcosxytan,任意角的三角函数的定义过程：AB)0,1(例1求的正弦、余弦和正切值35练习：将题目中的35改为67呢？yox解：在直角坐标系中，所以335tan,2135cos,2335sin353367tan,2367cos,2167sin，易知AOB与单位圆的交点坐标为的终边)23,21(.35AOB作例2已知角的终边经过点，求角的正弦、余弦和正切值.)4,3(0P则yMPPM,400xOMOM,3,0OMP00POM∽ysinxcosxytan于是，OPMPy1000OPPM;54OPOMx100OPOM;53.34),(yxPyox)4,3(0P.解：由已知得5)4()3(220OP设角的终边与单位圆交于点P),(yx，0MM0P分别过点作轴的垂线PxMP、、00PM练习：将点改为呢？0P)3,1(.3tan,21cos,23sin).0(tan,cos,sin2222xxyyxxyxy终边上任意一点的坐标也可以定义角的三角函数，并且三角函数值仅与角有关，与点在终边上的位置用角无关.P如果将点改为),(yxP呢？0P思考5.利用角的终边上任意一点定义角的三角函数三角函数定义域sincostan)(2ZkkRR2.确定三角函数值在各象限的符号yxosinyxocosyxotan+（）（）（）（）（）（）（）（）（）（）（）+++++归纳：一全正、二正弦、三正切、四余弦.1.根据三角函数的定义，确定它们的定义域（弧度制）探究例3确定下列三角函数值的符号：（1）250cos（2）)4sin(（3）3tan解：（1）因为250是第三象限角，（2）因为4是第四象限角，所以0)4sin(（3）因为tan)2tan(3tan，而的终边在x轴上，所以0tan0250cos所以⑴我们证明如果①②式都成立，那么为第三象限角.例4求证：当且仅当下列不等式组成立时，角为第三象限角.0tan0sin①②0sin因为①式所以角的终边可能位于第三或第四象限，也可能位于y轴的非正半轴上；因为①②式都成立，所以角的终边只能位于第三象限，为第三象限角.又因为②式0tan成立，所以或第三象限.角的终边可能位于第一为第三象限角时，不等式显然成立.⑵当证明：公式一：终边相同的角的同一三角函数的值相等.tan)2...