高中数学二轮复习 第23课时 极坐标与参数方程课件 新人教版 课件VIP免费

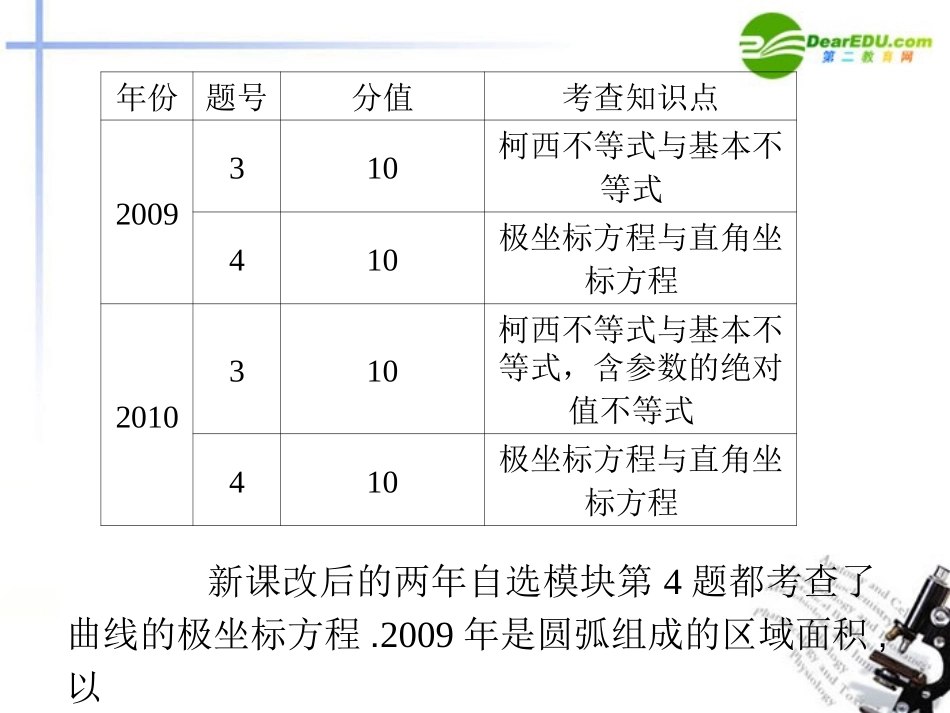
专题八自选模块年份题号分值考查知识点2009310柯西不等式与基本不等式410极坐标方程与直角坐标方程2010310柯西不等式与基本不等式，含参数的绝对值不等式410极坐标方程与直角坐标方程新课改后的两年自选模块第4题都考查了曲线的极坐标方程.2009年是圆弧组成的区域面积,以及直线与曲线的交点问题；2010年还是三段弧组成的封闭图形的面积和交点问题.可见直线和圆的极坐标方程是考查热点,解析法研究问题是重要的解决手段.参数方程在近两年高考中均未涉及．近两年自选模块第3题均考查了运用柯西不等式与基本不等式证明不等式或求最值问题,其中还需与函数求最值的其他方法相结合,有一定的难度.2010年还考查了解含参数的绝对值不等式的问题，必须对参数进行讨论,要求考生增强分类讨论的能力．柯西不等式与基本不等式是浙江高考自选模块第3题的考查重点和热点,另外也要注意绝对值不等式的性质,以及含参数的各类不等式的求解,要重视分类讨论的能力．考虑到极坐标的特点,直线和圆的极坐标方程将仍然是极坐标方程这块的考查重点；参数方程是2010年自选模块第4题的考查重点,要注意参数方程(特别是直线的参数方程)中参数的几何意义.直线的参数方程是考查的难点．22200001cos2.sintan,021()cos()sin1xxyxyyxxxyrxxryyr互化的前提：①极点与直角坐标系的原点重合；②极轴与轴的正方向重合；③两种坐标系中取相同的长度单位．互化公式，．圆心在，，半径为的圆的．极坐标参数与直角坐标的互方程为：为参数化．000000000022222()cos()sin()00.310cos()sinMxylxxtyyttlMMxyMMMMMMtMMtxyababxayb�过定点，，倾斜角为的直线的参数方程为：为参数．其中表示直线上以定点为起点，任意一点，为终点的有向线段的数量，当点在的上方时，；当点在的下方时，椭圆的一个参数方程为：为参数．224202()21ypxpxpttyptytxt抛物线的参数方程为：为参数．由于，因此参数的几何意义是抛物线上的点与抛物线的顶点连线的斜率的倒数．(20)sin()403.121AlmmmPlQOPOPOQQ�在极坐标系中，已知点，到直线：的距离为求实数的值；设是直线上的动点，在线段上，且满足，求点的轨迹方程，并指出轨迹是例1什么图形．m将极坐标方程转化为直角坐标方程，再利用点到直线的距离公式求得的值；极坐标系下的轨迹方程的求解与直角坐标系下的轨迹方程的求解方法类似，此处可用动点转移分析：法解决．0000001(20)|22|20.21321sin()2.4(,),(,).21.1xAlmmxymAldmlPQ：以极点为原点，极轴为轴的正半轴，建立直角坐标系，则点的直角坐标为，，直线的直角坐标方程为因为到直线的距离，由得直线的方程为设析，则解所以①220000()sin()2221()().8816131(.411sin()2sin)444()424xyQPlrQ因为点，在直线上，所以②将①代入②，得，即．这就是点的轨迹方化为直角坐标方程为因此点的轨迹是以，为圆心，为程．半径的圆．直角坐标与极坐标互化要注意互化的前提．若要判断曲线的形状，可先将极坐标方程化为直角坐标方程，再判断．在直角坐标系中，求曲线的轨迹方程的方法有直译法，定义法，动点转移法．在极坐标系中，求曲线的极坐标方程，这几种方法仍然是适用的．123123124sin()4234cos(2)4224(0)212(4)2,0(0)242()t(a2010)nOxCCCCCCMNCCABOABMN如图，在极坐标系中，已知曲线：:；:或；:．求由曲线，，围成的区域的面积；设，，，射线，与曲线，分别交于，不同于极点两点．若线段的中点恰好落在直线上变，浙江卷求式训练的值．2222211122422.122(2)241142464.422()2sin2cos2OSPABSSSABGONG弓形阴影部分由已知，所...