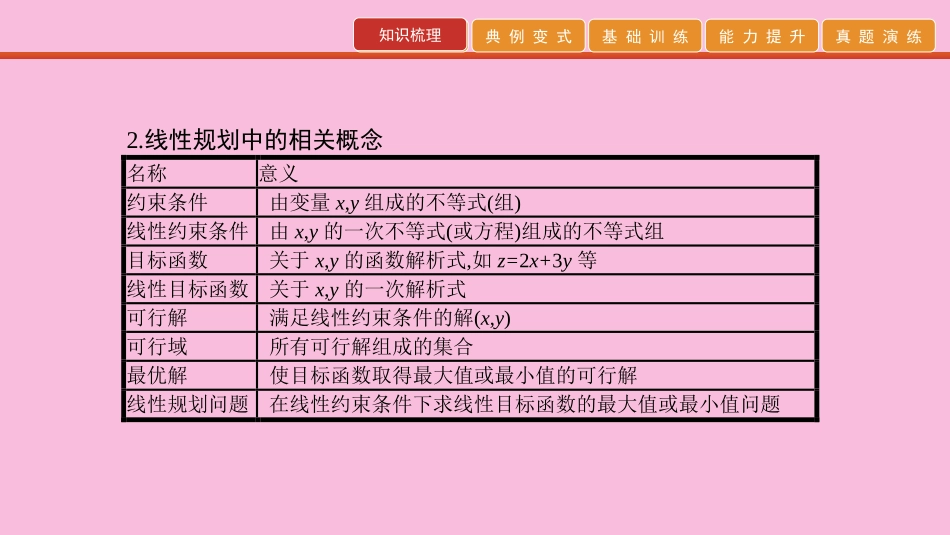
知识梳理典例变式基础训练能力提升真题演练第8讲简单的线性规划知识梳理典例变式基础训练能力提升真题演练知识梳理1.二元一次不等式(组)表示的平面区域不等式表示区域Ax+By+C>0直线Ax+By+C=0某一侧的所有点组成的平面区域不包括边界直线Ax+By+C≥0包括边界直线不等式组各个不等式所表示平面区域的公共部分知识梳理典例变式基础训练能力提升真题演练知识梳理2.线性规划中的相关概念名称意义约束条件由变量x,y组成的不等式(组)线性约束条件由x,y的一次不等式(或方程)组成的不等式组目标函数关于x,y的函数解析式,如z=2x+3y等线性目标函数关于x,y的一次解析式可行解满足线性约束条件的解(x,y)可行域所有可行解组成的集合最优解使目标函数取得最大值或最小值的可行解线性规划问题在线性约束条件下求线性目标函数的最大值或最小值问题知识梳理典例变式基础训练能力提升真题演练知识梳理【常见结论】1.确定二元一次不等式表示的平面区域位置的方法把二元一次不等式Ax+By+C>0(<0)表示为y>kx+b或ykx+b,则平面区域为直线Ax+By+C=0的上方;若y0.知识梳理典例变式基础训练能力提升真题演练典例变式题型一二元一次不等式(组)表示的平面区域【例1】(1)不等式组൝𝑥≥0,𝑥+3𝑦≥4,3𝑥+𝑦≤4,所表示的平面区域的面积等于()A.32B.23C.43D.34(2)若不等式组൝𝑥-𝑦+5≥0,𝑦≥𝑎,0≤𝑥≤2,表示的平面区域是一个三角形,则a的取值范围是()A.a<5B.a≥7C.5≤a<7D.a<5或a≥7知识梳理典例变式基础训练能力提升真题演练典例变式(3)已知关于x,y的不等式组൝0≤𝑥≤2,𝑥+𝑦-2≥0,𝑘𝑥-𝑦+2≥0,所表示的平面区域的面积为3,则实数k的值为.【解析】(1)由题意得不等式组表示的平面区域如图阴影部分,Aቀ0,43ቁ,B(1,1),C(0,4),则△ABC的面积为12×1×83=43.故选C.知识梳理典例变式基础训练能力提升真题演练典例变式(2)如图,当直线y=a位于直线y=5和y=7之间(不含y=7)时满足条件,故选C.知识梳理典例变式基础训练能力提升真题演练典例变式(3)直线kx-y+2=0恒过点(0,2),不等式组表示的平面区域如图所示,则A(2,2k+2),B(2,0),C(0,2),由题意知12×2×(2k+2)=3,解得k=12.【答案】(1)C(2)C(3)12知识梳理典例变式基础训练能力提升真题演练典例变式【规律方法】确定二元一次不等式(组)表示的平面区域的方法(1)“直线定界,特殊点定域”,即先作直线,再取特殊点并代入不等式(组).若满足不等式(组),则不等式(组)表示的平面区域为直线与特殊点同侧的那部分区域;否则就对应与特殊点异侧的平面区域.(2)当不等式中带等号时,边界为实线,不带等号时,边界应画为虚线,特殊点常取原点.知识梳理典例变式基础训练能力提升真题演练典例变式变式训练一1.(2016·全国卷Ⅲ)设x,y满足约束条件൝2𝑥-𝑦+1≥0𝑥-2𝑦-1≤0𝑥≤1,则z=2x+3y-5的最小值为.-10【解析】可行域为△ABC及其内部,其中A(1,0),B(-1,-1),C(1,3),直线z=2x+3y-5过点B时取最小值-10.知识梳理典例变式基础训练能力提升真题演练典例变式2.(基础经典试题)已知O是坐标原点,点A(-2,1),若点M(x,y)为平面区域൝𝑥+𝑦≥2,𝑥≤1,𝑦≤2上的一个动点,则𝑂𝐴ሬሬሬሬሬԦ·𝑂𝑀ሬሬሬሬሬሬԦ的取值范围是()A.[-1,0]B.[-1,2]C.[0,1]D.[0,2]B【解析】 A(-2,1),M(x,y),∴z=𝑂𝐴ሬሬሬሬሬԦ·𝑂𝑀ሬሬሬሬሬሬԦ=-2x+y,作出不等式组对应的平面区域及直线-2x+y=0,如图所示.平移直线-2x+y=0,由图象可知当直线经过点N(1,1)时,zmin=-2+1=-1;经过点M(0,2)时,zmax=2.知识梳理典例变式基础训练能力提升真题演练典例变式3.(2016·浙江卷)若平面区域൝𝑥+𝑦-3≥0,2𝑥-𝑦-3≤0,𝑥-2𝑦+3≥0夹在两条斜率为1的平行直线之间,则这两条平行直线间的距离的最小值是()A.3ξ55B.ξ2C.3ξ22D.ξ5B知识梳理典例变式基础训练能力提升真题演练典例变式【解析】画出不等式组所表示的平面区域如图所示,由൜𝑥-2𝑦+3=0,𝑥+𝑦-3=0,得A(1,2),由൜2𝑥-𝑦-3=0,𝑥+𝑦-3=0,得B(2,1).由题意可知当斜率为1的两条直线分别过点A和点B...