高中数学 223向量数乘运算及其几何意义课件 新人教A版必修4 课件VIP免费

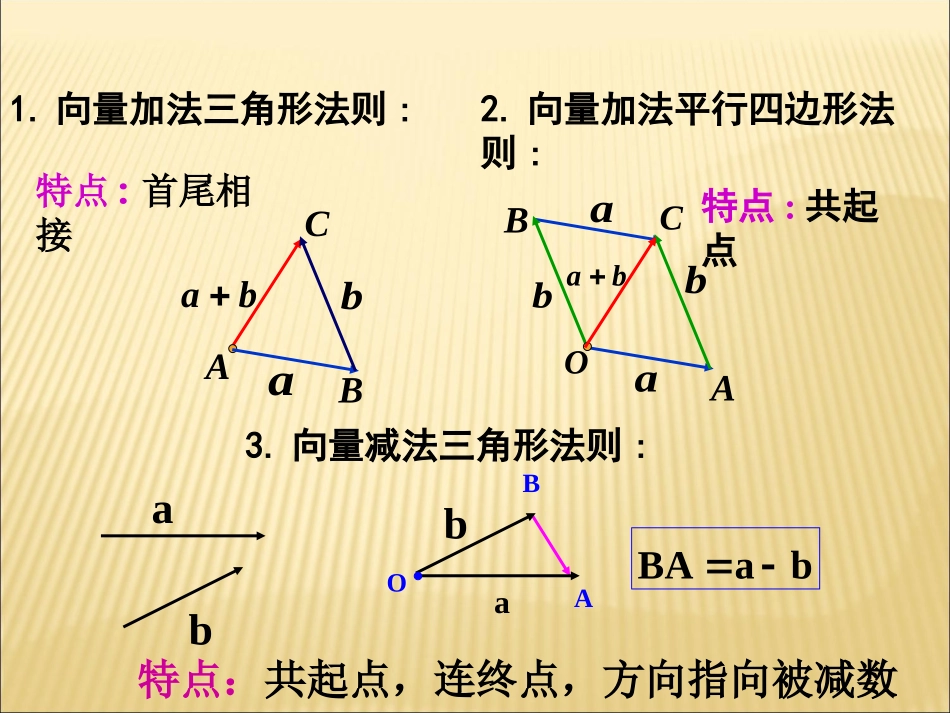
1.向量加法三角形法则:aAbBCbaaaAbBbOCba特点:首尾相接特点:共起点babBaABAab�2.向量加法平行四边形法则:3.向量减法三角形法则:O特点：共起点，连终点，方向指向被减数思考题1:已知向量如何作出和a,aaa(a)(a)(a)?aOAaBaCaNMQPaaaOCOAABBCaaa�记:aaa3a即:OC3a.�同理可得:PN(a)(a)(a)3a�思考题2:向量与向量有什么关系?向量与向量有什么关系?3aaa3a(1)向量的方向与的方向相同,向量的长度是的3倍,即3aaa3a3a3a.(2)向量的方向与的方向相反,向量的长度是的3倍,即3aa3aa3a3a.一、实数与向量的积的定义：如下：，它的长度和方向规定的积是一个向量，记作与向量实数aaaa1的方向相同；的方向与时，当aa02的方向相反；的方向与时，当aa0.000aa时，或当特别地，是无意义的．－，＋但不可以作加减法，即，可以作积，与向量实数aaa注意：二、实数与向量的积的运算律：aa)()(?6)2(3aaa2)2(3aa6aaaa)(a5a2a3?32)32(aaaa二、实数与向量的积的运算律：?222babaababa2b2baba22baba)(二、实数与向量的积的运算律：任意实数，则有：为、为任意向量，设ba,babaaaaaa)((3))((2))()((1)二、实数与向量的积的运算律：)2(3)3(2)3()2()3()2(43)((1)cbacbaababaa12a5b52abc注：向量与实数之间可以像多项式一样进行运算.例1：计算题)0(.1aaa有何关系？与是共线向量吗？，那么如果baab,.2？那么是共线向量，与如果abba3.想一想：2)可以是零向量吗?思考:1)为什么要是非零向量?三、共线向量基本定理：向量与非零向量共线当且仅当有唯一一个实数，使得ababab定理的应用:(1)有关向量共线问题:BCAB33BCAB3AC3DEADAE解：∴与共线．ACAE例2:如图：已知试判断与是否共线．ACAE，，33BCDEABADABCDE)0(三点共线、、CBABCBCAB(2)证明三点共线的问题:定理的应用:(1)有关向量共线问题:例3：设a，b是两个不共线的向量，求证：A，B，D三点共线.证明：又它们有公共点B∴A,B,D三点共线bababaCDBCBD5382AB5ABBD//，，，382baCDbaBCbaAB(2)证明三点共线的问题:定理的应用:(1)有关向量共线问题:////CDABCDABCDABCDAB直线直线不在同一直线上与(3)证明两直线平行的问题:)0(三点共线、、CBABCBCAB解：例4:在四边形ABCD中，求证：四边形ABCD为梯形．，2baAB，，354baCDbaBC28baCDBCABADBC2BCAD直线直线//BCAD//不在同一直线上与CDAB所以四边形ABCD为梯形练习035,.4bxaxbax解方程为不共线向量，为未知向量，设小结1.向量数乘的定义3.向量共线基本定理4.定理的应用2.向量数乘的运算律作业:1.阅读教材的相关内容2.教材第页第题3.红对勾的相关练习