高中数学 132(函数的极值与导数)课件 新人教B版选修2-2 课件VIP免费

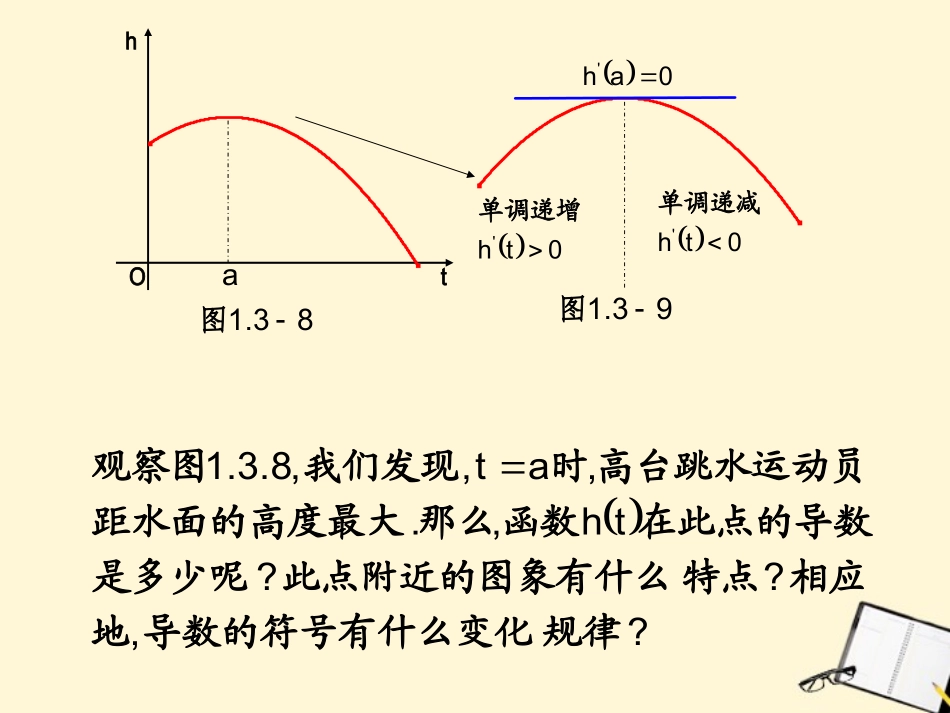
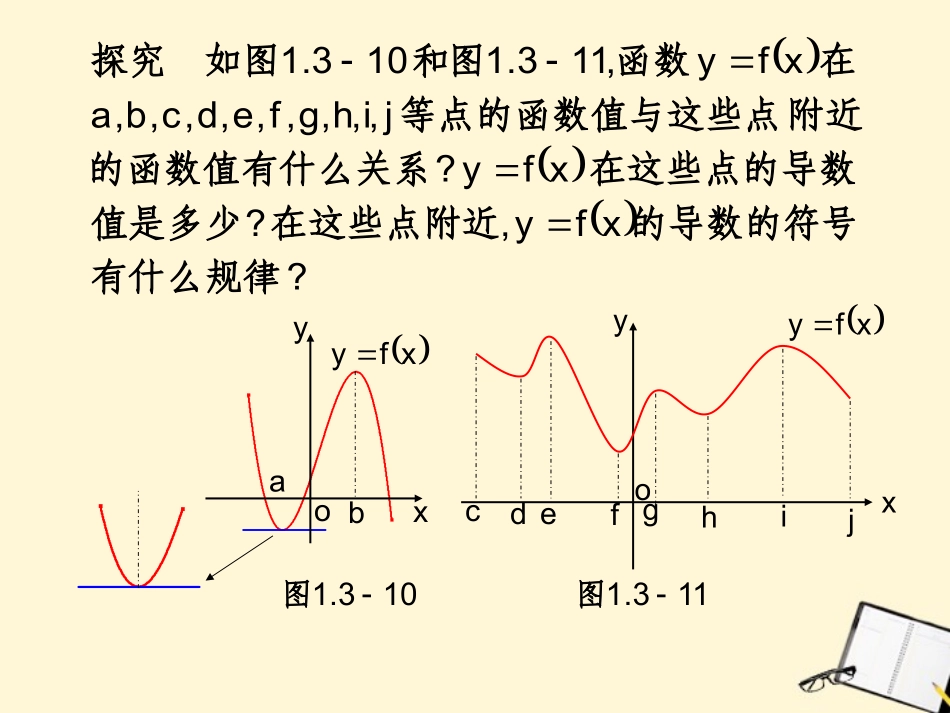
1.3.2函数的极值与导数?,??th,.,at,,8.3.1规律导数的符号有什么变化地相应特点此点附近的图象有什么是多少呢在此点的导数函数那么距水面的高度最大高台跳水运动员时我们发现观察图thOa83.1图0th'单调递增0th'单调递减0ah'93.1图?xfy,?xfy?j,i,h,g,f,e,d,c,b,axfy,113.1103.1有什么规律的导数的符号在这些点附近值是多少在这些点的导数的函数值有什么关系附近等点的函数值与这些点在函数图和如图探究cdefoghijxyxfyaboxyxfy103.1图113.1图aboxyxfy103.1图.0xf,0xfax;0af,axafaxxfy,,b,a'''右侧近的左侧附而且在点点的函数值都小附近其他它在点比的函数值点在函数以发现我们可两点为例以.0xf,0xfbx;0bf,bxbfbxxfy,'''右侧附近的左侧而且在点大都值的函数点其他附近在点比它的函数值在点函数类似地aboxyxfy103.1图;xfyaf,xfya的叫做函数的极小值点叫做函数我们把点极小值;xfybf,xfyb的函数叫做的极大值点叫做函数点极大值.valueextreme.极小值统称极大值和称为极小值点、极大值点统极值点极值.,的是函数的局部性质刻画点附近的大小情况极值反映了函数在某一.4x4x31xf43的极值求函数例.2x2x4xxf,4x4x31xf2'3所以因为解.2x,2x,0xf'或得令:下面分两种情况讨论;2x,2x,0xf1'时或即当.2x2,0xf2'时即当:xf,xf,x'的变化情况如下表变化时当单调递增单调递减单调递增34328xf00xf,222,222,x';3282f,xf,2x,并且极大值为值有极大时当因此.32f,xf,2x4极小值为并且有极小值时当.123.14x4x31xf3所示的图象如图函数?吗极大值一定大于极小极?0点吗的点一定是函数的极值导数值为思考22oxy4x4x31xf3123.1图.,xfy0xfy,.xxf0x,xxf,0xf,0x,0x,00f.x3xf,xxf,.033''2'3而非充分条件件在这点取极值的必要条是函数在一点的导数值为函数一般地极值点不是函数所以是单调递增的即函数恒有还是于无论但由虽然我们有函数对于例如值点的点不一定是函数的极导数值为;xf,0xf,0xfx1:0xf.0xf:xfy,0''00''是极大值那么右侧附近的左侧如果在时当解方程的极值的方法是求函数一般地.xf,0xf,0xfx20''0是极小值那么右侧附近的左侧如果在