高中数学 第七课时：切变变换课件 苏教版选修4-2 课件VIP免费

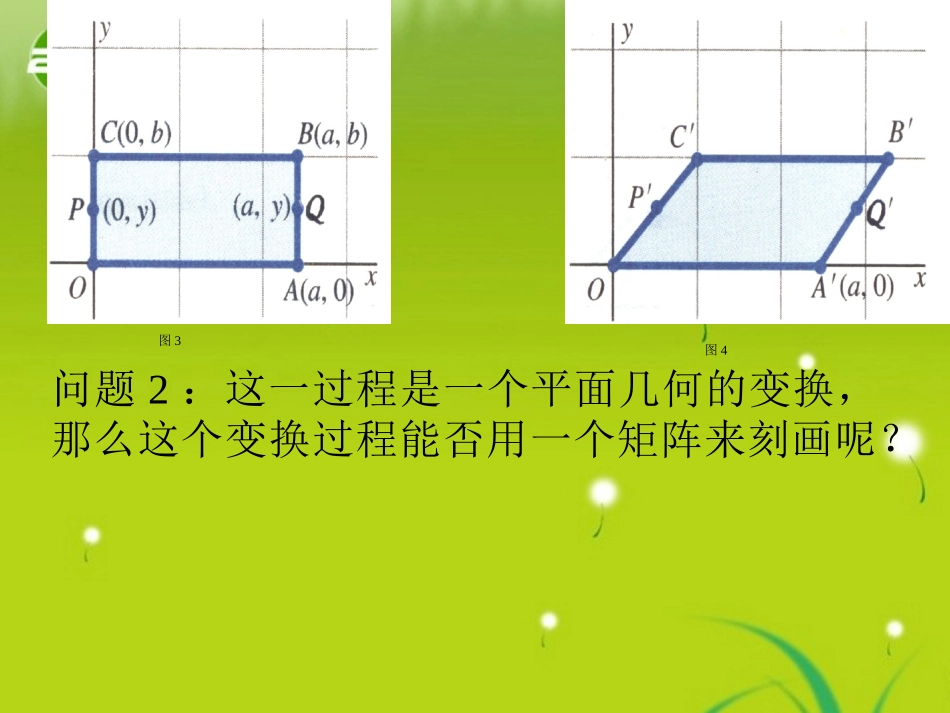
问题1：一副码好的纸牌，现将它的左边与一把直尺对齐，保持直尺底端右下角和最下面一张纸牌不动，用直尺轻轻推动纸牌，使得纸牌的形状变换为如图2所示的模样，问纸牌被推动的前后存在什么变化规律吗？图1图2问题情境：问题2：这一过程是一个平面几何的变换，那么这个变换过程能否用一个矩阵来刻画呢？图3图4切变变换切变变换探究：图3图41、切变变换有什么特征？O、A两点保持不变，其他点的纵坐标保持不变，横坐标都向右移动一定单位.图3图42、考察其中一个特殊点B:(,)(,)()BabBambmR:axTbyamb101mabb101mMb3M,,mkmkbb、在矩阵中，不妨设即一般地，对图中任意一点(x,y)，纵坐标保持不变，横坐标依纵坐标的比例增加，(,)(,)fxyxkyy:xxakyTkRyyb即，101kM11.P(,)01kxyx矩阵把平面上的点沿轴方向平移|ky|个单位.建构数学：切变变换、切变变换矩阵110011kk象由矩阵确定的变换通常叫做切变变换，对应的矩阵叫做切变变换矩阵。说明：0kyx时，沿轴正方向移动；0kyx时，沿轴负方向移动；ky=0时，原地不动，在此变换作用下，轴上点为不动点.2．是沿y轴方向的切变变换，对于原图形中的任意一点，横坐标保持不变，而纵坐标依横坐标的比例增加，它把平面上的点沿y轴方向平移|kx|个单位，101k当kx=0时，原地不动,在此变换作用下,轴上的点为不动点.当kx>0沿y轴正方向移动；当kx<0时，沿y轴负方向移动；1(2,0),(2,0),(2,2),(2,2)ABCD例、已知矩形的顶点⑴求矩形ABCD在矩阵作用下变换得到的几何图形.11201⑵求矩形ABCD在矩阵作用下变换得到的几何图形.10112例题应用：例2．如图所示，已知矩形ABCD在变换T的作用下变成图形，试求变换T对应的矩阵M。ABCD已知切变变换T使得矩形ABCD变为平行四边形试求变换对应的矩阵M，并指出矩形区域ABCD变换过程中的不变线段。ABCD练习：1(,)(,)(,)F,MF.xyxyxyy22例3、设圆F:x+y在对应切变变换下变换成另一图形试求变换所对应的矩阵及的解析式(,)(,)(,2)MFxyxyxyx变：变换为，求变换所对应的矩阵及的解析式.2xy1101求直线在矩阵作用下变换得到的几何图形的解析式.A(-2,0),B(0,1)C(0,-1),A(-2,-3),B(0,1),C(0,-1).ABCABC求把变为的变换，其中练习：试以切变变换矩阵和平行四边形ABCD为例加以说明，其中1101(0,0),(2,2),(6,2),(4,0).ABCD对于一个平面图形来说，在切变变换前后，它的几何性质（如线段长度、角度、周长、面积）有变化吗？思考：回顾反思：1．切变变换与切变变换矩阵的概念；101k2．是沿x轴方向的切变变换，x轴上的点是不动点。101k3．是沿y轴方向的切变变换，y轴上的点是不动点。4．切变变换保持图形面积不变。