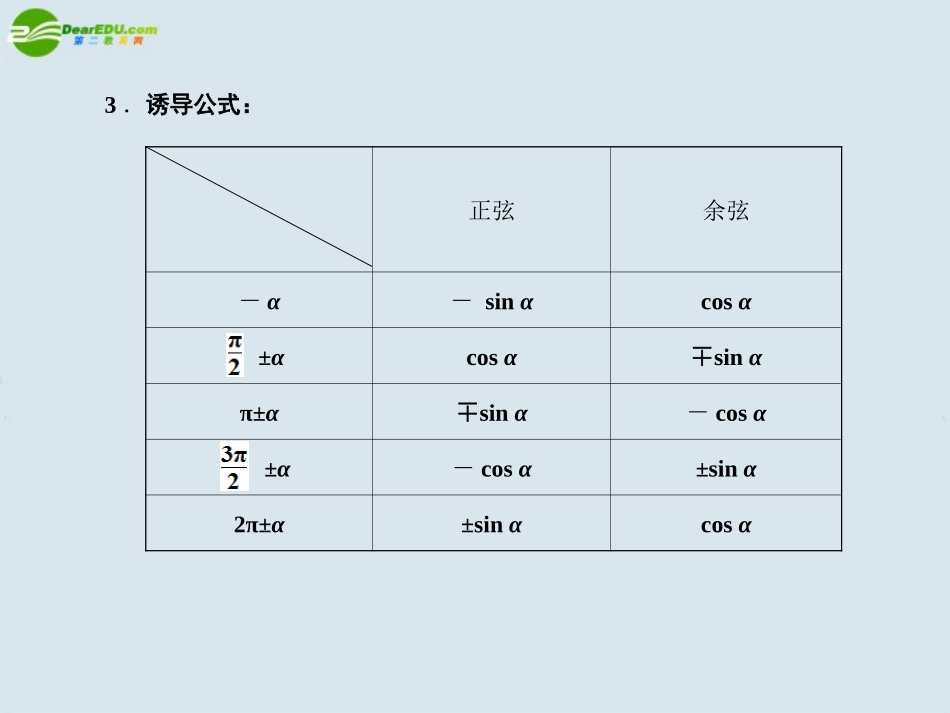
能利用单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式/理解同角三角函数的基本关系式3.2同角三角函数间的基本关系与诱导公式1.商数关系:=.2.平方关系:sin2α+cos2α=.tanα13.诱导公式:正弦余弦-α-sinαcosα±αcosα∓sinαπ±α∓sinα-cosα±α-cosα±sinα2π±α±sinαcosα1.(2009·全国Ⅰ)sin585°的值为()解析:sin585°=sin(360°+225°)=sin225°=sin(180°+45°)=-sin45°=-.答案:A2.(2009·陕西)若tanα=2,则的值为()A.0B.C.1D.解析:答案:B答案:A4.若sinθ=-,tanθ>0,则cosθ=________.解析:∵∴角θ在第三象限,cosθ=-答案:1.已知sinα,求cosα,tanα;2.已知cosα,求sinα,tanα;3.已知tanα,求sinα,cosα.上述三类问题都要使用平方关系,在进行开方运算时要注意其符号的确定,必要时要分情况讨论,特别应注意分类的标准和原则.【例1】求sinα、tanα的值:(1)cosα=-;(2)cosα=m(|m|≤1).解答:(1)∵cosα=-<0,∴α是第二或第三象限角.当α是第二象限角时,当α是第三象限角时,(2)当|m|=1时,α=kπ(kZ)∈,此时sinα=0,tanα=0;当m=0时,α=kπ+(kZ)∈,sinα=±1,tanα不存在;当0<|m|<1时,若α是第一、二象限的角,则sinα=,tanα=;若α是第三、四象限的角,则sinα=-,tanα=-.变式1.已知tanα=m,求sinα.解答:若m=0,则α=kπ,k∈Z,∴sinα=0.若α在一、二象限,sinα==;若α在第三、四象限,sinα=.解决三角函数问题的出发点是统一角、统一函数,降低次数,注意符号,而同角三角函数间的基本关系可以达到“统一函数”的目的,上述两种类型可借助商数关系和平方关系进行三角函数的“弦化切”.【例2】已知<α<π,tanα+cotα=-.(1)求tanα的值;(2)求的值.解答:(1)<∵α<π,∴-10,∴(sinx-cosx)2=1-2sinxcosx=.又sinx-cosx<0,∴sinx-cosx=-;【方法规律】1.在利用同角三角函数的基本关系式进行求值、化简、证明时,(1)如果函数种类比较多,可考虑切、割化弦;(2)要特别注意平方关系的使用,如“1”的代换技巧和消去等.2.可考虑使用平方关系和商数关系进行“弦化切”;可利用平方关系根据整体代入的思想方法进行sinαcosα与sinα+cosα和sinα-cosα的互相转化,同时注意方程思想的应用.3.诱导公式的记忆方法是:函数名不变、符号看象限(或奇变偶不变、符号看象限).(2009·全国Ⅱ)已知△ABC中,cotA=-,则cosA=()答案:D【答题模板】解析:【分析点评】1.本题是教材中已知tanA,求cosA的改编题,可考虑先求cos2A的值,然后求cosA.这样可直接通过平方关系和商数关系进行“弦化切”,达到解题方法的最优化.2.也可考虑利用已知条件和平方关系sin2A+cos2A=1,通过解方程组求cosA的值.点击此处进入作业手册