高中数学(空间直角坐标系)课件8 北师大版必修2 课件VIP免费

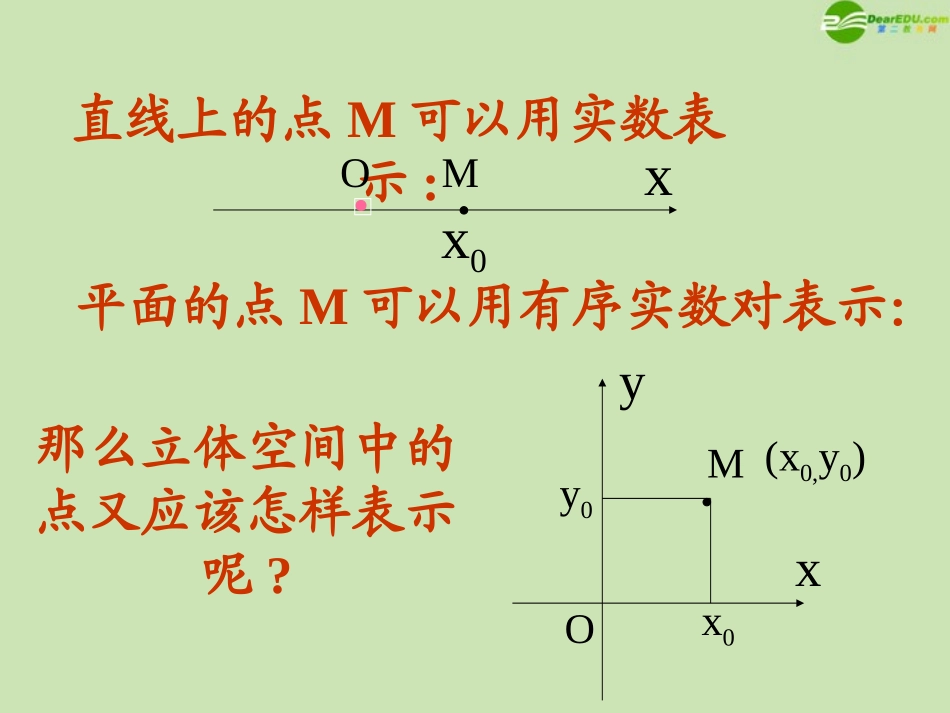
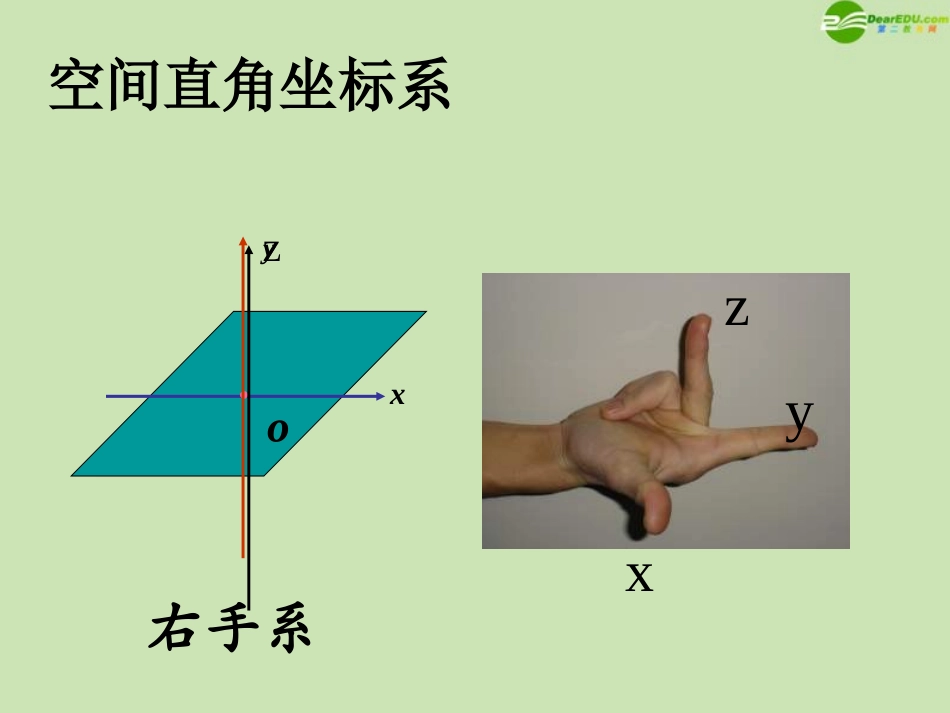
空间直角坐标系M直线上的点M可以用实数表示:平面的点M可以用有序实数对表示：yxO(x0,y0)xOMx0x0y0那么立体空间中的点又应该怎样表示呢?xoyz右手系空间直角坐标系yzxxyzox0z0y0MMyxO(x0,y0)x0y0(x0,y0,z0)平面的点M用实数对表示：空间坐标系中的点M的坐标用有序实数组(x0,y0,z0)来表示其中:x0是点M的横坐标,y0是点M纵坐标,z0是点M的竖坐标例1,如图:长方形OABC-DEFG中,|OA|=3,|OC|=4,|OD|=2.试写出O,A,G,F四点的坐标.xyzoADCBGEF解:如图O点坐标为(0,0,0)A点为(3,0,0)G点为(0,4,2)F点为(3,4,2)Ⅶxyozxoy面yoz面zox面空间直角坐标系共有八个卦限ⅠⅡⅢⅣⅤⅥⅧ设),,(1111zyxM、),,(2222zyxM为空间两点xyzo1MPNQR2M?21MMd在直角21NMM及直角PNM1中，使用勾股定理可以求得距离二、空间两点间的距离,121xxPM,12yyPN,122zzNM22221NMPNPMd.21221221221zzyyxxMM空间两点间距离公式特殊地：若两点分别为,),,(zyxM)0,0,0(OOMd.222zyxxyzo1MPNQR2M例1求证以)1,3,4(1M、)2,1,7(2M、)3,2,5(3M三点为顶点的三角形是一个等腰三角形.解221MM,14)12()31()47(222232MM,6)23()12()75(222213MM,6)31()23()54(22232MM,13MM原结论成立.例2设P在x轴上，它到)3,2,0(1P的距离为到点)1,1,0(2P的距离的两倍，求点P的坐标.解设P点坐标为),0,0,(x因为P在x轴上，1PP22232x,112x2PP22211x,22x1PP,22PP112x222x,1x所求点为).0,0,1(),0,0,1(空间直角坐标系空间两点M1(x1,y1,z1)与M2(x2,y2,z2)间的距离公式:（注意它与平面直角坐标系的区别）三、小结21221221221zzyyxxMM点的坐标的表示作业:1)P146练习1,练习22)P144练习.P147习题在练习本上完成