高中数学 131 柱体、锥体、台体、球体体积课件 新人教版必修2 课件VIP免费

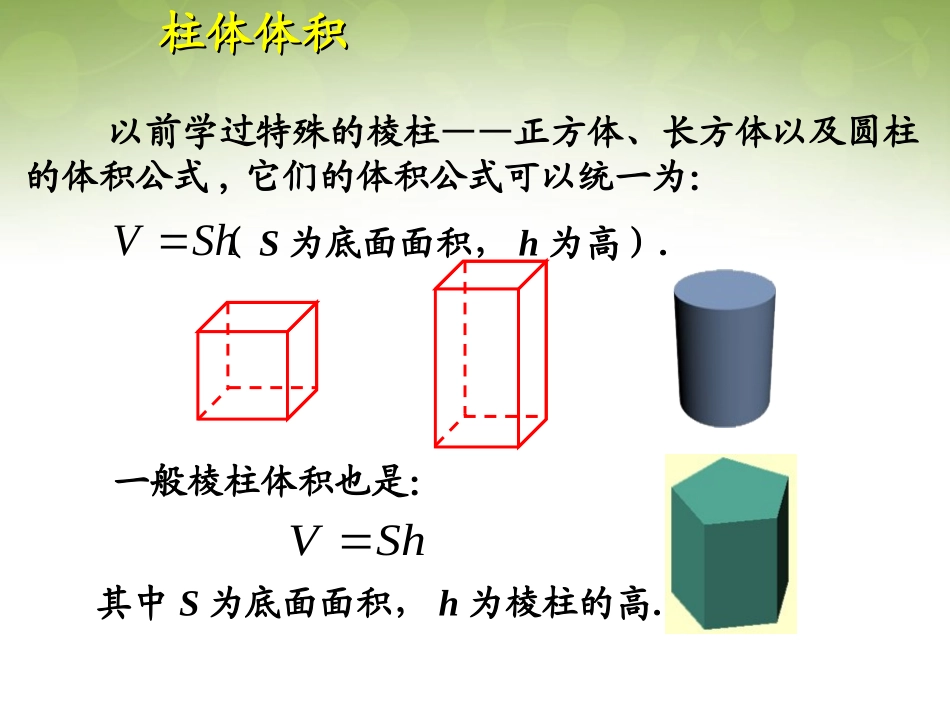
1.3.11.3.1柱体、锥体、台体，球体的体积柱体、锥体、台体，球体的体积以前学过特殊的棱柱——正方体、长方体以及圆柱的体积公式,它们的体积公式可以统一为：ShV（S为底面面积，h为高）．柱体体积柱体体积一般棱柱体积也是：ShV其中S为底面面积，h为棱柱的高．圆锥的体积公式：ShV31（其中S为底面面积，h为高）圆锥体积等于同底等高的圆柱的体积的．31圆锥体积圆锥体积ShV31（其中S为底面面积，h为高）由此可知，棱柱与圆柱的体积公式类似，都是底面面积乘高；棱锥与圆锥的体积公式类似，都是等于底面面积乘高的．31经过探究得知，棱锥也是同底等高的棱柱体积的．即棱锥的体积：31锥体体积锥体体积台体体积台体体积由于圆台(棱台)是由圆锥(棱锥)截成的，因此可以利用两个锥体的体积差.得到圆台(棱台)的体积公式(过程略)．根据台体的特征，如何求台体的体积？ABABCDCDPSShDCBAPABCDPVVVhSSSS)(31其中，分别为上、下底面面积，h为圆台（棱台）的高．SS柱体、锥体、台体的体积公式之间有什么关系？hSSSSV)(31S为底面面积，h为柱体高ShV0SS分别为上、下底面面积，h为台体高ShV31SSS为底面面积，h为锥体高台体体积台体体积上底扩大上底缩小例3有一堆规格相同的铁制（铁的密度是）六角螺帽共重5.8kg，已知底面是正六边形，边长为12mm，内孔直径为10mm，高为10mm，问这堆螺帽大约有多少个（取3.14）？3/8.7cmg解：六角螺帽的体积是六棱柱的体积与圆柱体积之差，即:10)210(14.3106124322V)(29563mm)(956.23cm所以螺帽的个数为252)956.28.7(10008.5（个）答：这堆螺帽大约有252个．典型例题典型例题如果用油漆去涂一个乒乓球和一个篮球，且涂的油漆厚度相同，问哪一个球所用的油漆多？为什么？实际问题实际问题一个充满空气的足球和一个充满空气的篮球，球内的气压相同，若忽略球内部材料的厚度，则哪一个球充入的气体较多？为什么？实际问题实际问题334RVR的球的体积为：定理：半径是球的体积球的体积球的表面积球的表面积24RSR的球的表面积为：定理：半径是例4：圆柱的底面直径与高都等于球的直径.求证：（1）球的体积等于圆柱体积的（2）球的表面积等于圆柱的侧面积..32(1)若球的表面积变为原来的2倍,则半径变为原来的倍.(2)若球半径变为原来的2倍，则表面积变为原来的倍.(3)若两球表面积之比为1:2，则其体积之比是.(4)若两球体积之比是1:2，则其表面积之比是.2422:134:1随堂练习随堂练习影响球的表面积及体积的只有一个元素，就是球的半径.柱体、锥体、台体的体积ShV31锥体hSSSSV)(31台体柱体ShV'SS0'S知识小结知识小结球的体积球的体积球的表面积球的表面积334RV24RS