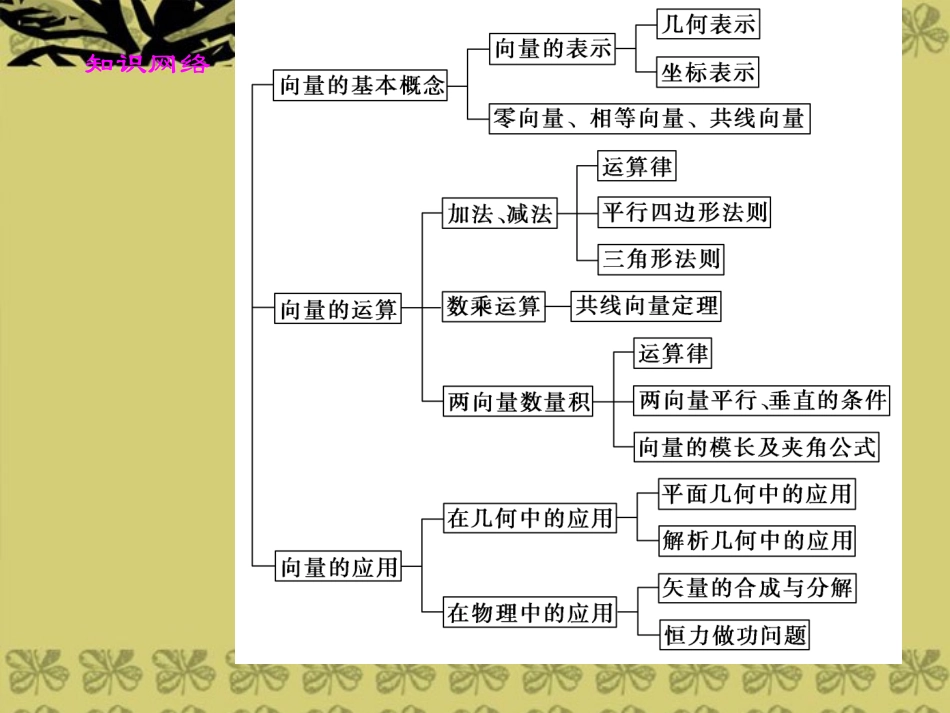
本章归纳整合知识网络要点归纳1.向量的概念及向量间的关系(1)向量是既有大小又有方向的量,用有向线段来表示,有向线段的长度即向量的模(长度),需注意有向线段有起点,而向量是自由移动的.(2)零向量长度为0,单位向量长度为1,二者方向都是任意的;相等向量是长度相等方向相同的向量;相反向量是长度相等方向相反的向量;平行(共线)向量是方向相同或相反的向量,与长度无关.(3)关于零向量的有关规定①0=0,-0=0(所有零向量相等,零向量的相反向量是零向量)②0∥a(零向量与任意向量共线)③0+a=a(零向量与任意向量a的和仍是a)④0a=0,λ0=0(零乘任何向量得零向量,任意实数乘零向量得零向量)⑤0·a=0(零向量与任意向量的数量积为0)⑥0=(0,0)(零向量的坐标表示中,横、纵坐标都是0)2.线性运算法则(1)向量加法是由三角形法则定义的,要点是“首尾相连”,即AB→+BC→=AC→;向量加法的平行四边形法则:将两向量移至共起点,分别为邻边作平行四边形,则这两邻边所夹的对角线所在向量即为向量的和.加法满足交换律、结合律.(2)向量减法实质是向量加法的逆运算,是相反向量的应用.几何意义有两个:一是以减向量的终点为起点,被减向量的终点为终点的向量;二是加法的平行四边形法则的另外一条对角线的向量.注意两向量要移至共起点.减法也满足交换律、结合律.(3)数乘运算即通过实数与向量的乘积,实现同向或反向上向量长度的伸缩变换.数乘向量满足结合律和分配律.3.共线定理与平面向量基本定理(1)共线向量定理:向量a(a≠0)与b共线,当且仅当有唯一一个实数λ,使得b=λa.共线向量定理是证明平行的主要依据,也是解决三点共线问题的重要方法.特别地,平面内一点P位于直线AB上的条件是存在实数x,使AP→=xAB→(或xAC→),或对直线外任意一点O,有OP→=xOA→+yOB→(x+y=1).(2)平面向量基本定理:如果向量e1,e2不共线,那么对于平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.其中e1,e2是平面的一组基底,e1,e2分别称为基向量.由定理可知,平面内任一向量都可以用两个不共线的向量表示出来,而且任意两个不共线的非零向量都可以作为基底.平面向量基本定理是实现平面任意向量的基底化表示,是平面向量坐标化表示的理论基础.4.向量数量积的运算及坐标表示(1)两个向量的数量积是a·b=|a||b|·cosθ,θ为a与b的夹角.数量积满足运算律:①与数乘的结合律,即(λa)·b=λ(a·b);②交换律,即a·b=b·a;③分配律:即(a+b)·c=a·c+b·c.(2)向量运算的坐标表示:若a=(a1,a2),b=(b1,b2),则①a+b=(a1+b1,a2+b2);②a-b=(a1-b1,a2-b2);③λa=(λa1,λa2);④a·b=a1b1+a2b2;⑤a∥b⇔a1=λb1,a2=λb2(λ∈R),或a1b1=a2b2(b1≠0,b2≠0);⑥a⊥b⇔a1b1+a2b2=0;⑦|a|=a·a=a21+a22;⑧若θ为a与b的夹角,则cosθ=a·b|a||b|=x1x2+y1y2x21+y21·x22+y22;(3)平面内两点A(x1,y1),B(x2,y2)间的距离为|AB→|=x2-x12+y2-y12.专题一向量的线性运算向量的加法、减法和数乘向量的综合运算通常叫做向量的线性运算.主要是运用它们的运算法则、运算律,解决诸如三点共线、两直线平行、线段相等、求点或向量的坐标等问题,而理解相关概念,用基底或用坐标表示向量是基础.【例1】在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD交于点F.若AC→=a,BD→=b,则AF→=________.(用a,b表示AF→)解析如图所示,AD→=AO→+OD→=12a+12b,DC→=AC→-AD→=a-12a-12b=12a-12b. A、E、F共线,∴AF→=λAE→=λ(AD→+DE→).=λ12a+12b-b4=λ2a+λ4b.又 AF→=AD→+DF→=AD→+μDC→=12a+12b+μ12a-12b=1+μ2a+1-μ2b,∴λ2a+λ4b=1+μ2a+1-μ2b. 向量a、b不共线,由平面向量基本定理,得λ2=1+μ2,λ4=1-μ2,解得λ=43,故AF→=23a+13b.答案23a+13b专题二向量的坐标运算1.向量的坐标表示实际上是向量的代数表示.引入向量的坐标表示后,向量的运算完全化为代数运算,实现数与形的统...