高中数学(平面向量应用)课件 新人教A版必修4 课件VIP免费

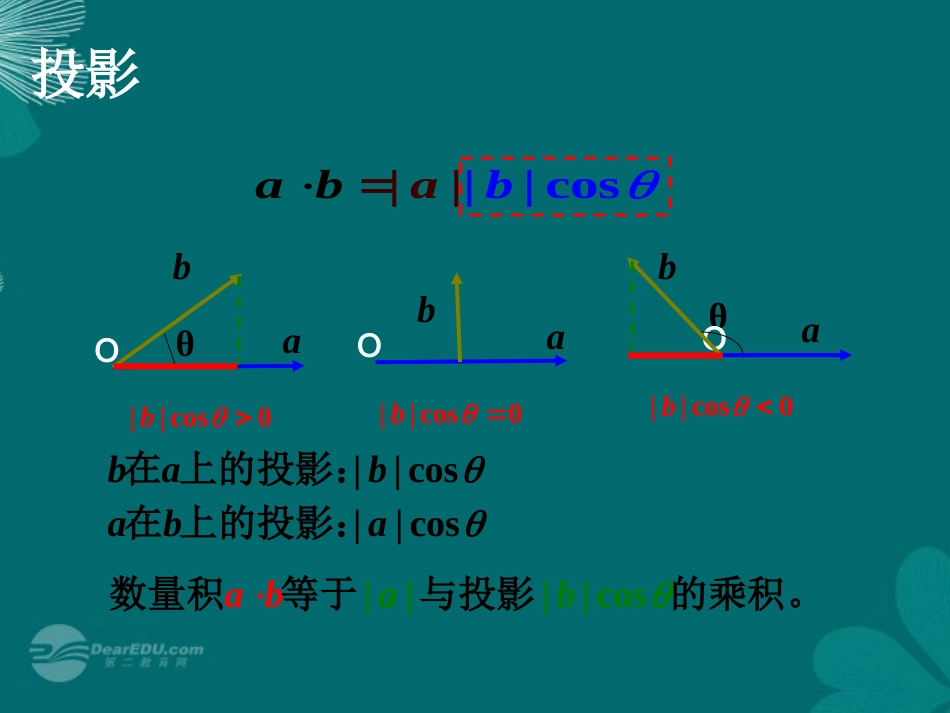
2.5平面向量应用举例向量的数量积已知两个非零向量与，它们的夹角为θ，我们把数量叫做与的数量积（或内积,点乘），ab|||cos|ab�ab||||cosababθO投影||||cosababOθab||cosbab在上的投影：||cos0bOab||cos0bab||cos0b||cosaba在上的投影：||||cosabba数量积等于与投影的乘积。复习||||cosabab(1)||5,||6,30abab，1531212xxyayb(2)(1,5),(3,2),abab7复习0abab22||aa?||||cosabab|||0cos9|ab|||0|ab0复习11ijxy2i2||i||1i||1j12j2||j1ij0ji0复习：坐标表示模(,),||axya已知求22||axy复习：.坐标表示向量垂直和平行1122(,),(,),axybxy则：121200ababxxyy1.向量垂直1221//0abbaxyxy2.向量共线坐标表示向量的夹角1122(,),(,)axybxycos||||abab121222221122xxyyxyxy例题：在△ABC中，，求8,7,60abCBCCA�解：ABC8760||8BC�||7CA�120120||||cos120BCCABCCA�187()282P123例1求证：平行四边形两条对角线的平方和等于相邻两边的平方和的两倍。DACB2||AB�,,ABaADb�证明：设2||a2||AD�2||b22||||ACab�2()ab222aabb2a2b22||||DBab�2()ab222aabb22||||ACDB�222()ab222()ABAD�原命题成立作业P127A4提示：22231212||||()FFFFF�