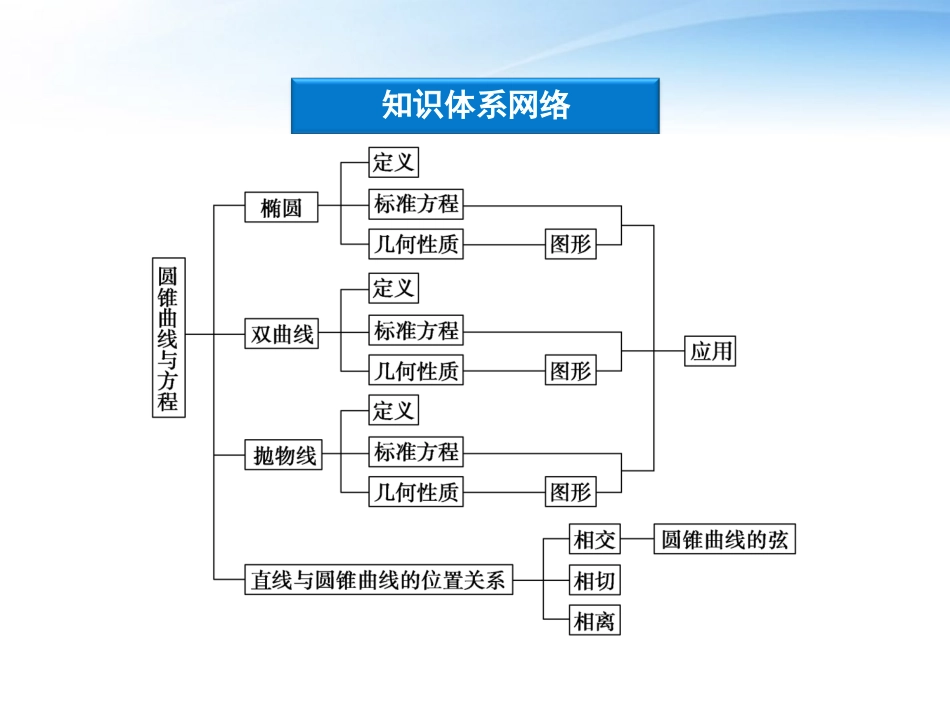
本章优化总结专题探究精讲本章优化总结知识体系网络知识体系网络专题探究精讲圆锥曲线的定义题型特点:对圆锥曲线定义的考查多以选择题和填空题形式出现,一般难度相对较小,若想不到定义的应用,计算量将会加大.解题时应注意应用.知识方法:(1)平面内满足|PF1|+|PF2|=2a(2a>|F1F2|)的点P的轨迹叫做椭圆,定义可实现椭圆上的点到两焦点的距离的相互转化.(2)平面内满足||PF1|-|PF2||=2a(2a<|F1F2|)的点P的轨迹叫做双曲线,|PF1|-|PF2|=2a(2a<|F1F2|)表示焦点F2对应的一支,定义可实现双曲线上的点到两焦点的距离的相互转化.(3)平面内与一个定点F和一条定直线l(不经过点F)距离相等的点的轨迹叫做抛物线,定义可实现抛物线上的点到焦点与到准线距离的相互转化.(2010年高考辽宁卷)设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为-3,那么|PF|=()A.43B.8C.83D.16例例11【解析】如图所示,直线AF的方程为y=-3(x-2),与准线方程x=-2联立得A(-2,43).设P(x0,43),代入抛物线方程y2=8x,得8x0=48,∴x0=6,∴|PF|=x0+2=8,选B.【答案】B圆锥曲线的性质题型特点:有关圆锥曲线的焦点、离心率等问题是考试中常见的问题,只要掌握基本公式和概念,并且充分理解题意,大都可以顺利求解.知识方法:圆锥曲线的简单几何性质(1)圆锥曲线的范围往往作为解题的隐含条件.(2)椭圆、双曲线有两条对称轴和一个对称中心,抛物线只有一条对称轴.(3)椭圆有四个顶点,对曲线有两个顶点,抛物线只有一个顶点.(4)双曲线焦点位置不同,渐近线方程不同.(5)圆锥曲线中基本量a,b,c,e,p的几何意义及相互转化.椭圆x2a2+y2b2=1(a>b>0)的焦距为2c,若直线y=2x与椭圆的一个交点的横坐标恰为c,则椭圆的离心率等于()A.2-22B.22-12C.3-1D.2-1例例22【解析】当x=c时,由c2a2+y2b2=1,得y=±b2a,所以2c=b2a=a2-c2a=a-c2a.因此,2ca=1-c2a2⇒e2+2e-1=0,解得e=-1±2.因为00,即m2<3k2+1①∴xP=xM+xN2=-3mk3k2+1,从而yP=kxP+m=m3k2+1,∴kAP=yP+1xP=-m+3k2+13mk,又|AM|=|AN|,∴AP⊥MN,则-m+3k2+13mk=-1k,即2m=3k2+1②把②代入①得2m>m2,解得00,解得m>12,故所求m的取值范围是(12,2).圆锥曲线中的定点、定值、最值问题题型特点:圆锥曲线中的最值、取值范围问题既是高考的热点问题,也是难点问题,解决这类问题的基本思想是建立目标函数和不等关系,根据目标函数和不等式求最值、取值范围,因此这类问题的难点就是如何建立目标函数和不等关系.知识方法:圆锥曲线中的定点、定值问题往往与圆锥曲线中的“常数”有关,如椭圆的长、短轴,双曲线的虚、实轴;抛物线的焦点等.可通过直接计算而得到.另外还可用“特例法”和“相关曲线系法”.圆锥曲线中的最值问题,通常有两类:一类是有关长度、面积等的最值问题;一类是圆锥曲线中有关几何元素的最值...