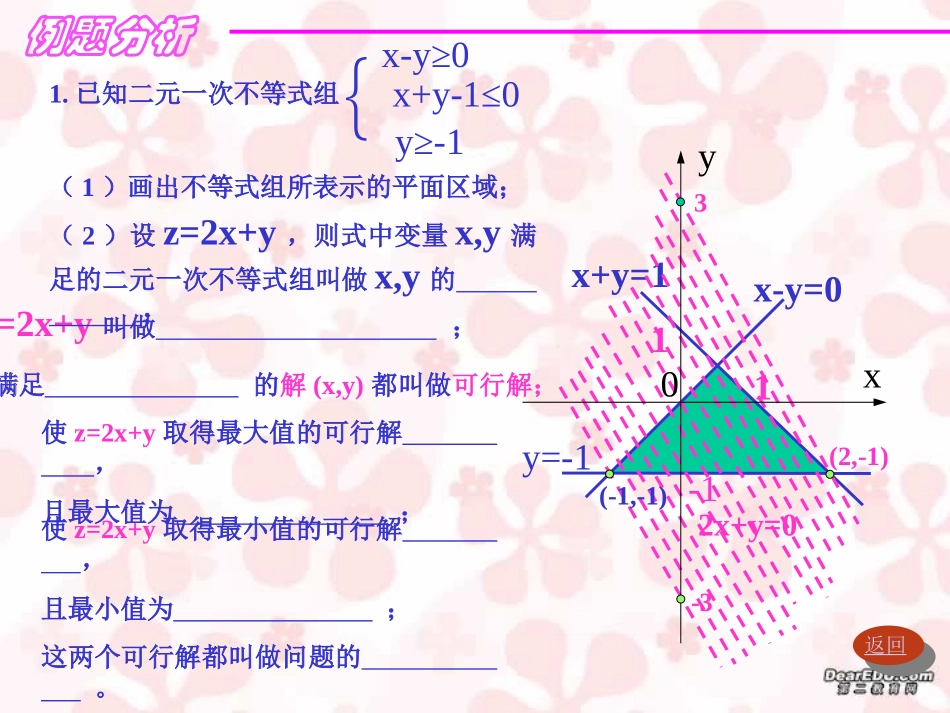
复习引入例题分析课堂练习课堂总结课题:线性规划例1解答例1解答网格线法网格线法调整优值调整优值练习1练习1练习2练习2例题总结例题总结使z=2x+y取得最大值的可行解,且最大值为;例题分析1.已知二元一次不等式组{x-y≥0x+y-1≤0y≥-1(1)画出不等式组所表示的平面区域;满足的解(x,y)都叫做可行解;z=2x+y叫做;(2)设z=2x+y,则式中变量x,y满足的二元一次不等式组叫做x,y的;y=-1x-y=0x+y=12x+y=0返回(-1,-1)(2,-1)3xy0使z=2x+y取得最小值的可行解,且最小值为;这两个可行解都叫做问题的。-311-1例题分析2.变量x,y满足线性约束条件2x+y-5≥03x-y-5≤0x-2y+5≥01)求z=2x-7y的最大值与最小值;2)求z=7x-2y的最大值与最小值;3)求z=2x+y的最大值与最小值;4)求z=2y/x的最大值与最小值;5)求z=x2+2x+y2+2y的最大值与最小值;例题分析3.设函数f(x)=ax2+bx,满足-1≤f(-1)≤2,2≤f(1)≤4,求f(-2)的范围.解:由已知条件得-1≤a-b≤2①2≤a+b≤4②∴①+②得①-②得1/2≤a≤30≤b≤5/2而f(-2)=4a-2b∴由不等式的性质得-3≤f(-2)≤12.错例题分析例1:某工厂生产甲、乙两种产品.已知生产甲种产品1吨需消耗A种矿石10吨、B种矿石5吨、煤4吨;生产乙种产品1吨需消耗A种矿石4吨、B种矿石4吨、煤9吨.每1吨甲种产品的利润是600元,每1吨乙种产品的利润是1000元.工厂在生产这两种产品的计划中要求消耗A种矿石不超过300吨、消耗B种矿石不超过200吨、消耗煤不超过360吨.甲、乙两种产品应各生产多少(精确到0.1吨),能使利润总额达到最大?返回分析:将已知数据列成下表:10543002004产品消耗量A种矿石(t)B种矿石(t)甲产品(1t)资源乙产品(1t)资源限制(t)煤(t)利润(元)493606001000设生产甲、乙两种产品.分别为x吨、y吨,利润总额为z元,那么{10x+4y≤3005x+4y≤2004x+9y≤360x≥0y≥0z=600x+1000y.例题分析解:设生产甲、乙两种产品.分别为x吨、y吨,利润总额为z元,那么{10x+4y≤3005x+4y≤2004x+9y≤360x≥0y≥0z=600x+1000y.作出以上不等式组所表示的可行域作出一组平行直线600x+1000y=t,解得交点M的坐标为(12.4,34.4)5x+4y=200{4x+9y=360由0xy10x+4y=3005x+4y=2004x+9y=360600x+1000y=0M答:(略)(12.4,34.4)返回经过可行域上的点M时,目标函数在y轴上截距最大.此时z=600x+1000y取得最大值.平移找解法904030405075例题分析例2要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:解:设需截第一种钢板x张,第一种钢板y张,则规格类型钢板类型第一种钢板第二种钢板A规格B规格C规格2121312x+y≥15,{x+2y≥18,x+3y≥27,x≥0,xN∈*y≥0yN∈*作出可行域(如图)目标函数为z=x+y今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。返回例题分析x0y2x+y=15x+3y=27x+2y=18x+y=02x+y≥15,{x+2y≥18,x+3y≥27,x≥0,xN∈*y≥0yN∈*经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.答:(略)作出一组平行直线t=x+y,目标函数t=x+y返回B(3,9)C(4,8)A(18/5,39/5)打网格线法在可行域内打出网格线,当直线经过点A时t=x+y=11.4,但它不是最优整数解,将直线x+y=11.4继续向上平移,7.51518279例题分析x0y2x+y=15x+3y=27x+2y=18x+y=02x+y≥15,{x+2y≥18,x+3y≥27,x≥0,xN∈*y≥0yN∈*直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.作出一组平行直线t=x+y,目标函数t=x+y返回C(4,8)A(18/5,39/5)当直线经过点A时t=x+y=11.4,但它不是最优整数解.作直线x+y=12x+y=12解得交点B,D的坐标B(3,9)和D(4.5,7.5)调整优值法B(3,9)D(4.5,7.5)7.51518279答(略)例题总结1.线性规划问题大致可以分为两种类型:一种是给定一定数量的人力、物力资源,问怎样安排这些资源能使完成任务量最大,收到的效益最大;第二类是给定一项任务,问怎样统筹安排,能使完成这项任务的人力,物力资源量最小。解决这两类问题的共同点是寻求在约束条件下,某项整体指标的最大值。2.线性规划问题可以按照下列步骤求解:找出全约束条件列出目标函数作出可行域求出最优解回答实际问题返回巩固练习xy02x+y-600=0600x+2y-9...