高中数学 向量的加法课件 新人教B版必修4 课件VIP免费

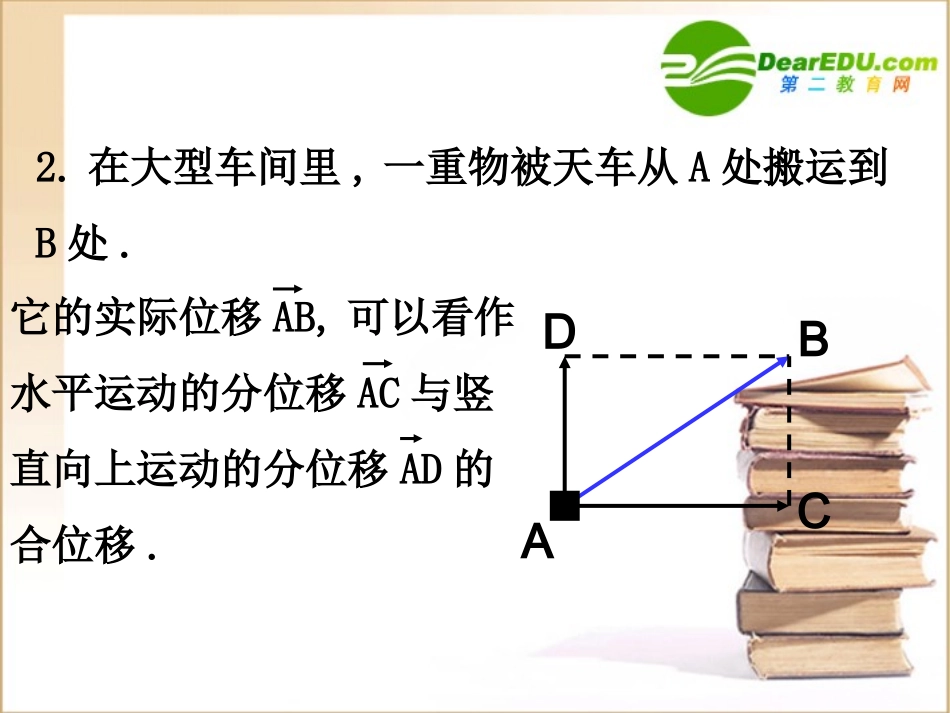
向量的加法向量的加法北京广州上海引入:1.飞机从广州飞往上海,再从上海飞往北京,这两次位移的结果与飞机从广州直接飞往北京的位移是相同的.这时我们就把后面这样一次位移叫做前面两次位移的合位移.AB2.在大型车间里,一重物被天车从A处搬运到B处.CD它的实际位移AB,可以看作水平运动的分位移AC与竖直向上运动的分位移AD的合位移.由分位移求合位移,称为位移的合成求两个向量和的运算叫向量的加法。ab向量的加法的定义：向量的加法的定义：求两个向量和的运算叫做求两个向量和的运算叫做向量的加法向量的加法..求两个向量和的运算叫做求两个向量和的运算叫做向量的加法向量的加法..baBba+baA���已知向量a和b,在平面内任取一点O,作OA=a,AB=b,则向量OB叫做a和b的和,记作a+b.即a+b=OA+AB=OBO两个向量的和仍是一个向量,当向量a与向量b不共线时，a+b的方向与a，b都不同向，且|a+b|<|a|+|b|．abA.BaCb作法：[1]在平面内任取一点Aba+根据向量加法的定义得出的求向量和的方法根据向量加法的定义得出的求向量和的方法,,称为称为首尾相连首尾连向量加法的三角形法则。向量加法的三角形法则。[2]作AB=a,BC=b[3]则向量AC叫作向量a与b的和，记作a＋b。注意代数表达式AB+BC=AC两种特例(两向量平行)ABC1.方向相同ababAC��当a与b同向时，则a+b，a，b同向，且|a+b|=|a|+|b|；两种特例(两向量平行)2.方向相反BCAababAC��当a与b反向时，若|a|>|b|，则a+b的方向与a相同，且|a+b|=|a|-|b|若|a|<|b|则a+b方向与b相同，且|a+b|=|b|-|a|这叫做向量加法的平行四边形法则。abAaBbDCa+b作法：作AB=a,AD=b,以AB，AD为邻边作平行四边形，则AC=a+b。共起点练一练如图,已知用向量加法的平行四边形法则作出baba,（1）abbbaababa（2）共起点baba+abba+bac+ab+()a+bc+(),.a如图，已知,,，请作出bcab+ab+cb+,,baccabcabbc向量加法的运算律①交换律：a+b=b+a②结合律：（a+b)+c=a+(b+c)cbaAaBCbDc向量加法的运算律向量加法的运算律交换律：交换律：abba结合律：结合律：()()abcabc想一想1.若两向量互为相反向量,则它们的和为多少?0aaaa（）（）00aaa2.零向量和任一向量的和为多少?a�AaBbDCa+b��a+b,a+b和a-b的大小关系如何?想一想ababab何时取得等号?≦≦ABCDEFO1(2)(3)OABCDEFOAOCBCFEOAFE�例1：已知为正六边形的中心，作出下列向量（）;1OBOCOA）解：（;2ADFEBC）（.03FEOA）（例2:求向量之和.�AB+DF+CD+BC+FA解: �=AB+BC+CD+DF+FA�=AC+CD+DF+FA�=AD+DF+FA�=AF+FA�=0�AB+DF+CD+BC+FA��∴AB+DF+CD+BC+FA=0)4()3()2()1(edcdbadcba１.化简________)1(BCCDAB________)2(CBACBNMA________)3(DCCABDAB２.根据图示填空abcdefgABDECcfgfADMN0巩固练习:例3:如图，一艘船从A点出发以的速度向垂直于对岸的方向行驶，同时河水以2km/h的速度向东流求船实际行驶速度的大小与方向23km/hCBA解:如图,设用向量表示船向垂直于对岸的速度,用向量表示水流的速度�AC�ABD以AC,AB为邻边作平行四边形,则就是船实际行驶的速度�ADCBADo∴∠DAB=60答:船实际行驶速度的大小为4km/h,方向与水流速度间的夹角.o60�在Rt△ABD中,AB=2,BD=23� AD=AB+BD�∴AD=4∴tan∠DAB=3练习1轮船从Ａ港沿东偏北方向行驶了40海里到达B处,再由B处沿正北方向行驶40海里到达C处.求此时轮船与A港的相对位置.30°东北AB30C��图设别轮两则轮解：如，AB、BC分表示船的次位移,AC表示船的合位移,AC=AB+BC。��在Rt△ADB中,∠ADB=90°,∠DAB=30°,|AB|=40，所以|DB|=20,|AD|=203���2222在Rt△ADC中,∠ADC=90°,|DC|=60，所以|AC|=|AD|+|DC|=(203)+60=403, |AC|=2|AD|∴∠CAD=60°。D练习2两个力F1和F2同时作用在一个物体上,其中F1=40N,方向向东,F2=40N,方向向北,求它们的合力.3东北OBθC12,.,,.OAFOBFOAACOACBOCF��解：如图，表示表示以为邻边作平行四边形则表示合力122222,||40N||||403N.,F||||||4034080Rt...