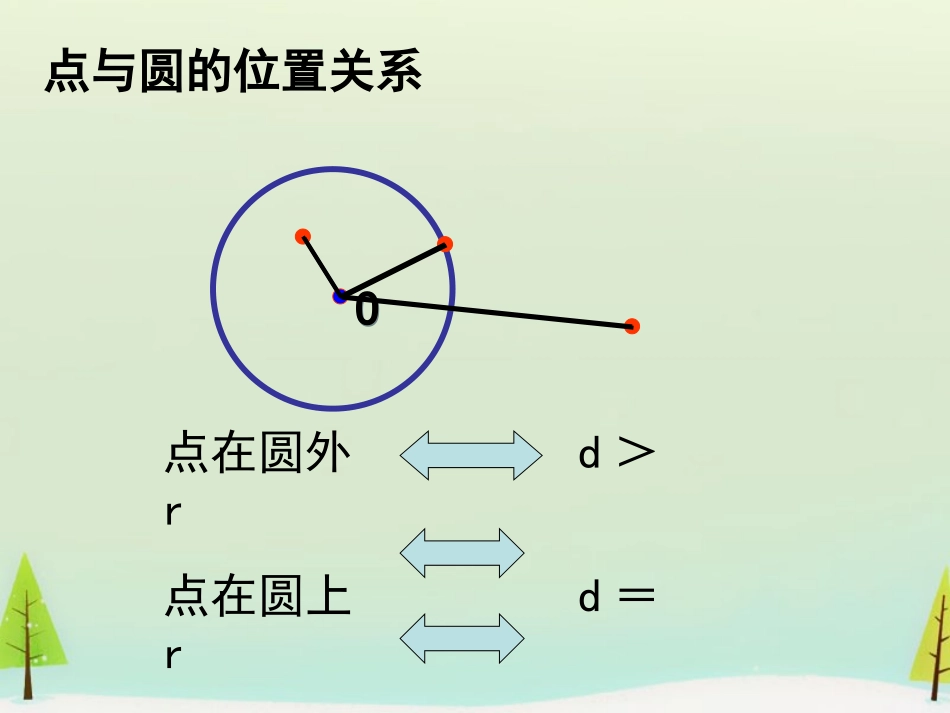
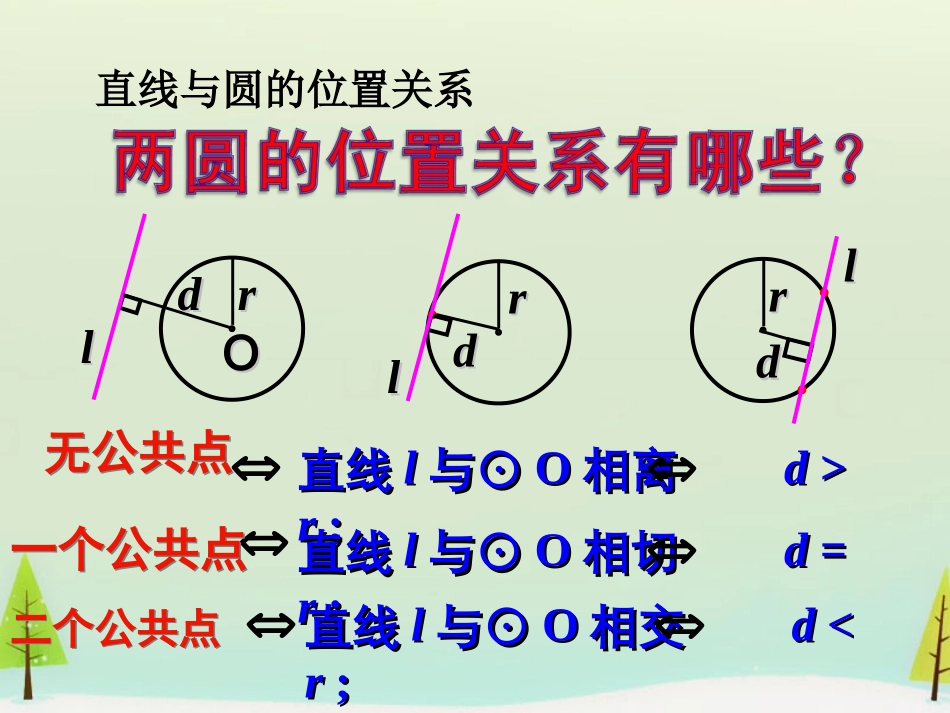
点与圆的位置关系点在圆外d>r点在圆上d=r点在圆内d<rOOrrrrrrddOOllddllddll直线直线ll与⊙与⊙OO相离相离dd>>rr;;直线直线ll与⊙与⊙OO相切相切dd==rr;;直线直线ll与⊙与⊙OO相交相交dd<R+rR+r>d>|R-r|d<|R-r|两圆位置关系的性质与判定位置关系d和R、r关系交点两圆外离d>R+r0两圆外切d=R+r1两圆相交R−rd0性质判定0R―rR+r同心圆内含外离外切相交内切d1、⊙O1和⊙O2的半径分别为3cm和4cm,求⊙O1和⊙O2的位置关系.设:(1)O1O2=8cm______(2)O1O2=7cm________(3)O1O2=5cm_______(4)O1O2=1cm_______(5)O1O2=0cm_______外离外切相交内切内含2、判断下列圆与圆的位置关系:(1)圆1)2()3(22yx与圆36)1()7(22yx的位置关系是(2)圆1)2()2(22yx与圆16)5()2(22yx的位置关系是3、圆6422yx与圆02213022xyx的公切线条数是条外切内切422122122220024440,xyxyxyxyCCC已知圆:与试判断圆与的位例1:置关系。222212:68110xymxyxym圆O与圆O:相交变式:,求实数的取值范围22122222821024(1)(2)xyxyxyxyC+CABAB|AB|.若圆:与圆:交于、两点.求:直线的方程;例2:22122122220024440,xyxyxyxyCCC已知圆:与试判断圆与的位例1:置关系。1222222222200(1)24440(2)(1)(2),23120(3)243541080(44)5xyxyxyxyxyyxxx=CC圆与圆解一-的方程联立,得到方程组得由(3)得将上式代入(1)整413(-108)=85理得13其判别式方程组有两组32>0故根:,两圆相交.2211222222121122127|(11)(21)13xyrxyRCC--CC|CC圆的方程化为()+()=22圆心(1,1),半径=圆的方程化为()+()=49圆心(1,2),半径=解二:22122122220024440,xyxyxyxyCCC已知圆:与试判断圆与的位例1:置关系。12722,722722137|22RRrRrRrr|CC且又故,两圆相交1222212346|5rmxyROOO|OO圆的圆心为(0,0),半径圆的标准方程为()+()=36圆的圆心为(-3,4),半径解:222212:68110xymxyxym圆O与圆O:相交变式:,求实数的取值范围12|1121|||6|56RrRrmmm-|OO解得两圆相交,即22122222821024(1)(2)xyxyxyxyC+CABAB|AB|.若圆:与圆:交于、两点,求:直线的方程;例2:122222228(1)21024(2)(1)(2),240xyxyxyxyxyABCC圆与圆的方程联立,得到方解:(1)这就是直线的直程组得线方程.221121211115250|124552|rdxyrABdCC|AB|=|AB|C=圆的标准方程为()+()=10圆的圆心为(-1,-1),半径到直线的距离2则得()【总结与提升】【总结与提升】22211112222222)())(),C-C-xaybrxaybrd1、已知两圆圆:(与圆:(的圆心距为则两圆外离;两圆外切;两圆相交;两圆内切;两圆内含2、当两圆的方程中22xy、系数相同时,将两圆方程相减即得所在的直线方程。公共弦12drr12drr1212||rrdrr12||drr12||drr【反馈检测】【反馈检测】1、若0