陕西省汉中市高一数学(空间直线与直线之间的位置关系) 课件VIP免费

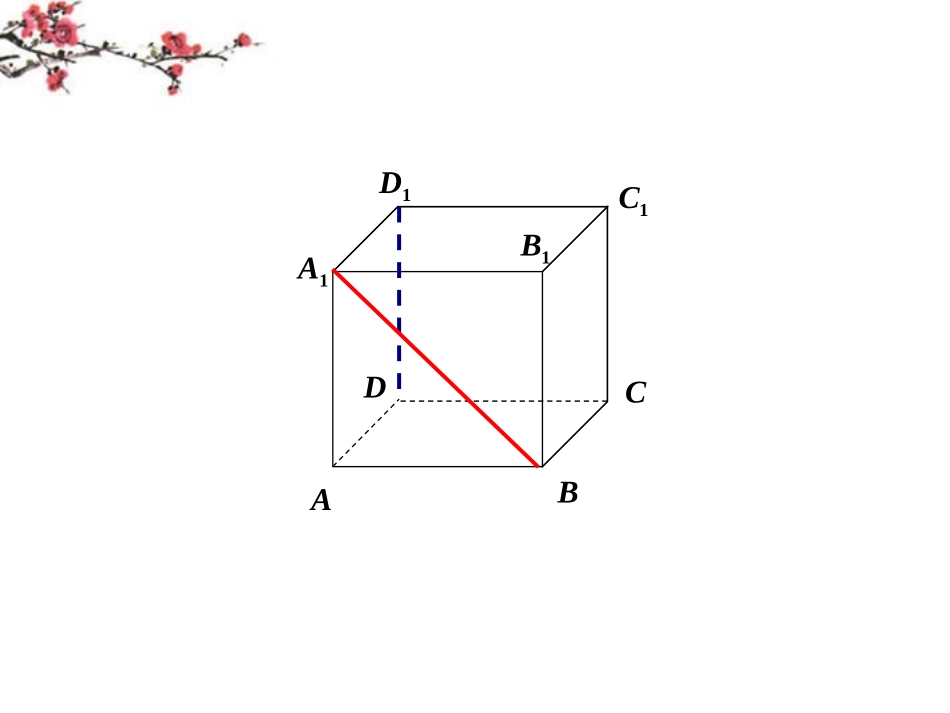
空间中直线与直线之间的位置关系D1DCBAC1B1A1.异面直线的定义:不同在任何一个平面内的两条直线叫做异面直线。11、空间两条直线的位置关系、空间两条直线的位置关系①①从有无公共点的角度：从有无公共点的角度：有且仅有一个公共点有且仅有一个公共点------------------相交直线相交直线在同一平面内在同一平面内----------------相交直线相交直线平行直线平行直线②②从是否共面的角度从是否共面的角度没有公共点没有公共点------------------平行直线平行直线异面直线异面直线不在同一平面内不在同一平面内------------------异面直线异面直线相交直线：共面、有且只有一个公共点平行直线：共面、没有公共点异面直线：不同在任何一个平面内没有公共点永远不具备共面的条件不能误解为分别在不同平面内的直线22、异面直线的画法、异面直线的画法αabαβbaαaba与b是相交直线a与b是平行直线a与b是异面直线abM答：不一定：它们可能异面，可能相交，也可能平行。分别在两个平面内的两条直线是否一定异面？abab33公理公理44平行于同一条直线的两条直线互相平行平行于同一条直线的两条直线互相平行直线直线aa，，bb，，cca∥bc∥ba∥c(直线平行的传递性)例3已知E、F、G、H分别是空间四边形四条边AB、BC、CD、DA的中点，求证：EFGH是平行四边形.44、、等角定理等角定理空间中如果两个角的两边分别对应平行，空间中如果两个角的两边分别对应平行，那么这两个角相等或互补那么这两个角相等或互补..推论：推论：如果两条相交直线和另两条相交直如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角线分别平行，那么这两组直线所成的锐角（或直角）相等（或直角）相等..两条异面直线所成的角1、怎样定义异面直线所成的角？ab设a、b为两异面直线，经过空间一点o作直线，我们把所成的锐角（或直角）叫做异面直线a与b所成的角（或夹角）.bbaa//,//ba与oaˊbˊ''Oab2、若点位置不同，则与所成的角的大小会发生变化吗？为什么？aba'b'oa‘’b‘’o'aO.O3、为了简便，点常取在两异面直线中的一条上ba'两条异面直线所成的角的范围：两条异面直线所成的角的范围：αabO如果两条两条异面直线所成的角是直角，那么称这两条异面直线互相垂直。ba记作角的范围角的范围::（（0°0°，，90°]90°]如图,已知长方体ABCD-EFGH中,AB=,AD=,AE=2(1)求BC和EG所成的角是多少度?(2)求AE和BG所成的角是多少度?2323解答：(1)GFBC∵∥∴∠EGF（或其补角）为所求.RtEFG△中，求得∠EGF=45o(2)BFAE∵∥∴∠FBG（或其补角）为所求,RtBFG△中，求得∠FBG=60o5.课堂练习ABGFHEDC23232【例【例11】在正方体】在正方体ABCD-AABCD-A11BB11CC11DD11中中,,棱长为棱长为44(1)(1)求直线求直线BABA11和和CCCC11所成的角的大小所成的角的大小(2)(2)若若MM，，NN分别为棱分别为棱AA11BB11和和BB11BB的中点，的中点，求直线求直线AMAM与与CNCN所成的角的余弦值所成的角的余弦值..四、例题选讲四、例题选讲A1B1C1D1ABCDMNPQBQ=1BN=2QN=5QC=17NC=52Cos∠QNC=522222NCQNQCNCQN异面直线的求法:一作(找)二证三求