高中数学：412 极坐标系1)课件(新人教选修4-4) 课件VIP免费

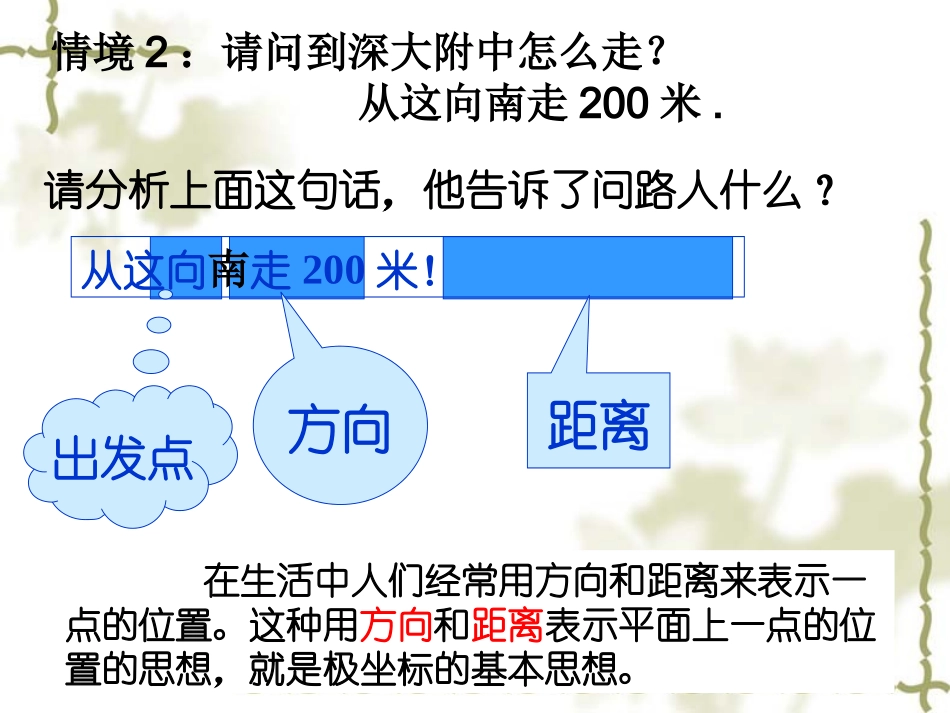
教学目标:1.理解极坐标的概念2.学会用极坐标表示平面上的点教学重点:1.理解极坐标的意义2.能够在极坐标系中用极坐标确定点位置问题2：如何刻画这些点的位置？一、问题情境情境1：军舰巡逻在海面上，发现前方有一群水雷，如何确定它们的位置以便将它们引爆？情境2：请问到深大附中怎么走？从这向南走200米。问题1：为了简便地表示上述问题中点的位置，应创建怎样的坐标系呢？请分析上面这句话，他告诉了问路人什么？从这向南走200米！出发点方向距离在生活中人们经常用方向和距离来表示一点的位置。这种用方向和距离表示平面上一点的位置的思想，就是极坐标的基本思想。情境2：请问到深大附中怎么走？从这向南走200米.1、极坐标系的建立：在平面内取一个定点O，叫做极点.引一条射线OX，叫做极轴。再选定一个长度单位和角度单位及它的正方向（通常取逆时针方向）.这样就建立了一个极坐标系.XO二、新知学习2、极坐标系内一点的极坐标的规定对于平面上任意一点M,用表示线段OM的长度,用表示以射线OX为始边,射线OM为终边所成的角,叫做点M的极径,叫做点M的极角,有序数对(,)就叫做M的极坐标。XOM极点的极坐标为_________________(0,),可为任意值.思考:对比直角坐标系，比较异同(1)要素：________________________________________；(2)平面内点的极坐标用_____表示.极点、极轴、长度单位、角度单位和正方向(,)例1.如图，写出各点的极坐标：。Ox42564353A•B•C•D•E•F•G•A(4,0)B(3,)4C(2,)2D(5,)56E(4.5,)F(6,)43G(7,)53(3,0)(6,2)(3,)245(5,)(3,)(4,)365(6,)3ABCDEFG[变式训练1]在课本P6的图上描下列点：[小结]由极坐标描点的步骤：(1)先按极角找到点所在射线；(2)在此射线上按极径描点.3、点的极坐标的表达式的研究XOM如图：OM的长度为4，4请说出点M的极坐标的其他表达式思考：这些极坐标之间有何异同？思考：这些极角有何关系？这些极角的始边相同，终边也相同。也就是说它们是终边相同的角。本题点M的极坐标统一表达式：π42kπ+4，极径相同，不同的是极角思考:①平面上一点的极坐标是否唯一？若不唯一,那有多少种表示方法？②不同的极坐标是否可以写出统一表达式？4、极坐标系下点与它的极坐标的对应情况[1]给定（,）,就可以在极坐标平面内确定唯一的一点M[2]给定平面上一点M，但却有无数个极坐标与之对应。原因在于：极角有无数个。OXPM(ρ,θ)如果限定ρ＞0,0≤θ＜2π那么除极点外,平面内的点和极坐标就可以一一对应了.例2.在极坐标系中,(1)已知两点，，求线段PQ的长度；(2)已知点M的极坐标为(,),R,说明满足上述条件的点M的位置.)3,5(P)34,2(Q4在一般情况下，极径都是取正值。但在某些必要的情况下，也允许取负值(<0):当<0时如何规定(,)对应的点的位置？°Ox当<0时，点M(,)的位置规定：))||•M(,)°OxM(-2,)56)56¬¬•点M：在角终边的反向延长线上，且|OM|=||M(-2,)565、关于负极径小结：从比较来看,负极径比正极径多了一个操作,将射线OP“反向延长”.。Ox425654531162332A(-4,0)C(-2,)2B(3,)56D(-1,)53E(3,-)6(-4,-)3F•A•B•C•D•E•F[小结](,)(,2k+)(-,+)[-,+(2k+1)]都是同一点的极坐标.例3.已知点Q(,)，分别按下列条件求出点P的坐标：(1)P是点Q关于极点O的对称点；(2)P是点Q关于直线的对称点.(3)P是点Q关于极轴的对称点。2注意点M的极坐标具有多值性.[3]一点的极坐标有否统一的表达式？三、小结[1]建立一个极坐标系需要哪些要素极点；极轴；长度单位；角度单位和它的正方向.[2]极坐标系内一点的极坐标有多少种表达式？无数，极角有无数个.有。（ρ，2kπ+θ）四、课后作业教材P14-15页5，8，9，10，11思考:极坐标系中,点M的坐标为(-10,),则下列各坐标中,不是M点的坐标的是()(A)(10,)(B)(-10,-)(C)(10,-)(D)(10,)433532323