高中数学中点弦课件 人教版 课件VIP免费

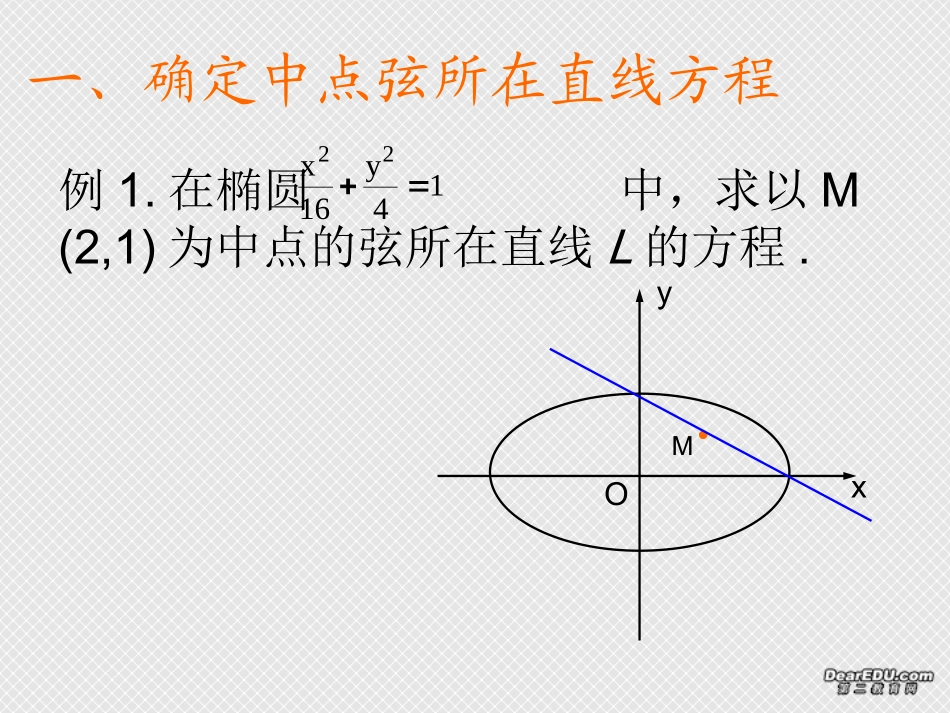
一、确定中点弦所在直线方程例1.在椭圆中，求以M(2,1)为中点的弦所在直线L的方程.14y16x22yOxM已知圆锥曲线的弦中点P(x0,y0),其斜率为k,探索它们的关系式P(x0,y0)k？？0)2py(px4.0)2px(py3.0)(by-ax2.b)a0,b0,1(abyax1.2222222222抛物线抛物线双曲线椭圆0022212122212122221222212222222212210022,11,2222yx)ab(-yyxx)ab(-x-xy-yk0by-yax-x1byax1byax),y,P(xAB),yB(x),yA(xb)a0,b0,1(abyax1.即两式相减得：则中点设弦端点椭圆练习：已知双曲线，试问是否存在被点B(I,I)所平分的弦？如果存在，求出弦所在直线的方程，如果不存在，说明理由。12y-x22解：假设存在这样的直线m,设其斜率为K，则2112yx12k00∴m方程:y-1=2(x-1),即2x-y-1=0但将2x-y-1=0代入双曲线方程并整理得：2x2-4x+3=0,判别式∆＝－8<0,∴直线m与双曲线相离，故满足题设条件的直线m不存在。OyBx二、求弦中点坐标例2.已知直线x-3y+1=0与椭圆相交于A、B，求弦AB中点的坐标。14y9x22解：设中点M(x0,y0)则即4x0+3y0=0又x0-3y0+1=0,得31yx)94(-k00)154,51M(-三、求平行弦中点轨迹例3.已知椭圆,求其斜率为2的平行弦中点的轨迹方程.1y2x22yOxM解法一：设平行弦所在直线方程y=2x+b,代入x2+2y2=2得:9x2+8bx+2b2-2=0,设弦端点A(x1,y1),B(x2,y2),中点M(x,y),则98b-xx219bb2xyb94-2xxx2104yxb,得：消去(在已知椭圆内）三、求平行弦中点轨迹例3.已知椭圆,求其斜率为2的平行弦中点的轨迹方程.1y2x22yOxM在已知椭圆内），则由点差法，得设弦中点解法二0(4yx2yx)21(-ky)M(x,:四、求过定点弦中点轨迹例4.已知椭圆，定点M(1,0),求过点M的动弦AB中点P的轨迹方程.1y4x22OMABP解:设P(x,y),则直线PM的斜率为1-x0-yyx)41(-k整理：x2-x+4y2=0巩固练习:1.椭圆被P(4,2)平分的弦所在直线L的方程为______________.2.直线y=x+1被椭圆x2+2y2=4截得的弦中点的坐标为____________.19y36x223.抛物线y=x2的一组斜率为2的平行弦中点轨迹方程是_____________.X+2y-8=0)31,32(-X=1（y>1）(在已知抛物线内）4.已知椭圆中心为原点，一个焦点为，截直线y=3x-2所得弦中点的横坐标为，求椭圆方程.)2F(0,521125x75y225.椭圆mx2+ny2=1与直线y=1-x交于M,N两点，原点与线段MN中点连线的斜率为，求的值.22nm221.中点弦问题基本解法:(1)利用韦达定理(2)点差法2.用点差法解决中点弦问题,其要点是用弦中点坐标表示弦的斜率,可化难为易,化繁为简;3.灵活运用数形结合思想、方程思想、化归思想解决直线与圆锥曲线位置关系问题.课堂小结:思考题：已知椭圆，试确定m的取值范围，使得对于直线y=4x+m,椭圆上有不同的两点关于该直线对称。13y4x22作业：1.已知椭圆，(1)若它的一条弦AB被M(1,1)平分，求AB所在直线的方程.(2)求过点M(1,1)的弦中点轨迹方程.14y16x222.已知椭圆中心在原点，以坐标轴为对称轴，它与直线x+y=1交于A,B两点，C是AB的中点，且|AB|=,OC的斜率为，求椭圆方程.2222谢谢各位老师的指导最后祝您一帆风顺