高中数学 221(平面向量基本定理)课件(2) 新人教B版必修4 课件VIP免费

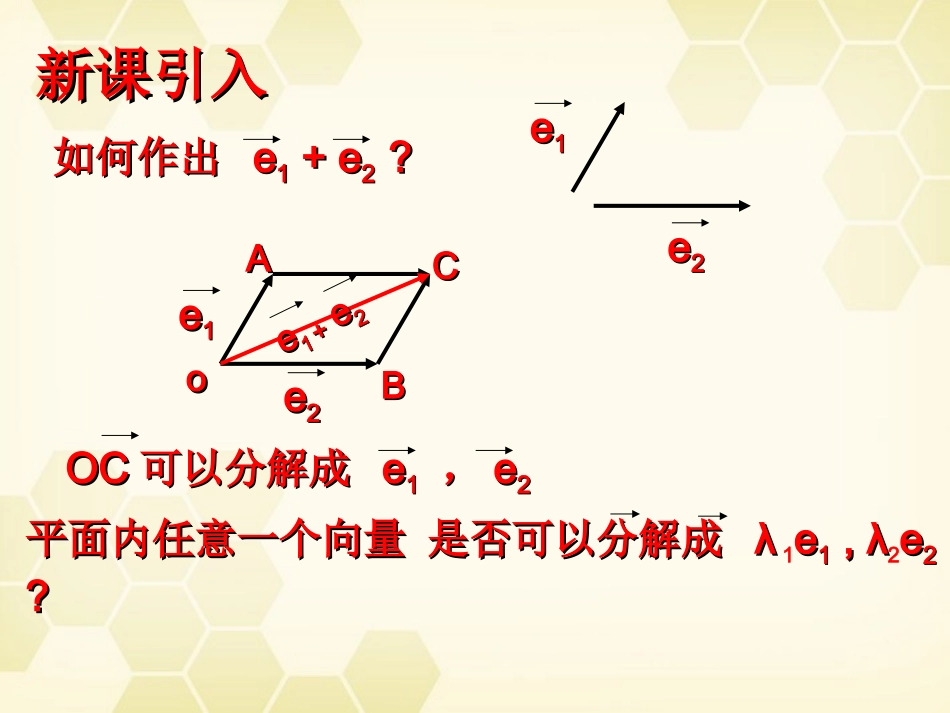
数学使人聪颖数学使人严谨数学使人深刻数学使人缜密数学使人坚毅数学使人智慧1.实数与向量的积3.如果两个向量的基线互相平行或重合，则称这些向量共线或互相平行.abcd1.aaaaa实数和向量的乘积是一个向量，记作，的长2.三角形法则；平行四边形法则不共线2.两向量和的求法3.平行向量及平行向量基本定理////0abababbab如果=，则；反之，如果，则一定存在一个实数，使=新课引入新课引入如何作出如何作出ee11+e+e22??ee11ee22ooAAee11BBee22CCee11ee22++OCOC可以分解成可以分解成ee11，，ee22平面内任意一个向量是否可以分解成平面内任意一个向量是否可以分解成λλ1ee11,,λλ2ee22??12,ee�是两个不平行向量，观察上图12CDee�12ABee�，12EFee�，12GHee�2344425事实上，平面内任何向量都能用两个不平行向量来表示.新课引入GHAEBDCF1e�2e�ee11ooAAoo11BBaaoo22CCee22ooAABBCCNNMMOMOM与与OAOA共线共线OM=OM=λλ11OA=OA=λλ11ee11同理同理ON=ON=λλ22OB=OB=λλ22ee22∴∴a=a=λλ11ee11++λλ22ee222.2.1平面向量基本定理定理内容：1212,,,eeaaa�如果和是一平面内的两个不平行的向量，那么该平面的任一向量存在惟一的一对实数使1122aaeae��1212112212,.,eeeeaeaeaee��不共线向量、叫做表示这一平面内所有向量的一组基底，记为叫做向量关于基底的分解式.几点说明：121ee�定理中的、是两不共线向量；122aaa是平面内的任一向量，且实数对、是惟一的；3平面内任一两个不共线的向量都可作为一组基底.例题教学例题教学例例11已知：向量已知：向量ee11，，ee22求作：求作：向量向量-2.5-2.5ee11+3+3ee22ee11ee22ooAABB-2.5-2.5ee1133ee22CC作法：作法：11、任取一点、任取一点OO作作OA=OA=-2.5-2.5ee11OB=OB=33ee2222、以、以OA,OBOA,OB为邻边作为邻边作OAOACBCB33、、OCOC为所求为所求1练习12,.eeABCDEFGH�在基底下，分解下列向量：、、、1e�2e�ABCDEFGH解：1222ABee�，1233CDee�1232EFee�，1263GHee�例例22已知：已知：ABCDABCD的两条对角线相交于点的两条对角线相交于点MM，，且且AB=a,AD=b,AB=a,AD=b,用用a,ba,b表示表示MA,MB,MC,MA,MB,MC,和和MDMDBBAACCDDMMbbaa分析：为了求分析：为了求MA,MB,MC,MDMA,MB,MC,MD只需求只需求AC,DBAC,DB即可即可解：,ACABADab�,DBABADab�1111,2222MAACabab�1111,2222MBDBabab�111,222MCACab�111.222MDDBab�AABBCCAA11练习211,ABpACqABCpqAA��已知：三角形ABC的两边对应的向量=,=,是中点写出在基底下，的分解式为提示：法一11AAABBA�法二112AAABAC�11122AApq�11,2BABC�BCACAB�例例33,ABlOllPtOPOAOB�已知、是直线上任意两点，是外一点，求证：对直线上任一点，存在实数，使关于基底的分解式为1OPtOAtOB�Pl并且，满足式的点一定在上.分析：分析：OP=OA+APOP=OA+AP或或OP=OB+BPOP=OB+BPBBOOAAPPl例例33证明：Pl设点在直线上，则由平行向量基本定理知，.tAPtABtOBOA�存在实数，使（）OPOAAP�所以OAtOBtOA�1.tOAtOB�1,POPtOAtOB�设点满足等式,OPOAtOAtOB�则OPOAtOBOA�即,APtAB�亦即//.APAB�故A又因为有公共点，ABP所以、、共线,Pl所以在直线上.BBOOAAPPl例例33,ABlOllPtOPOAOB�已知、是直线上任意两点，是外一点，求证：对直线上任一点，存在实数，使关于基底的分解式为1OPtOAtOB�Pl并且，满足式的点一定在上.BBOOAAPPl,lPt由例3所证可知，对直线上任意一点，一定存在惟一的实数,tlP满足向量等式，反之对每一个数值在直线上都有惟一的一个点与之对应；向量等式叫做...