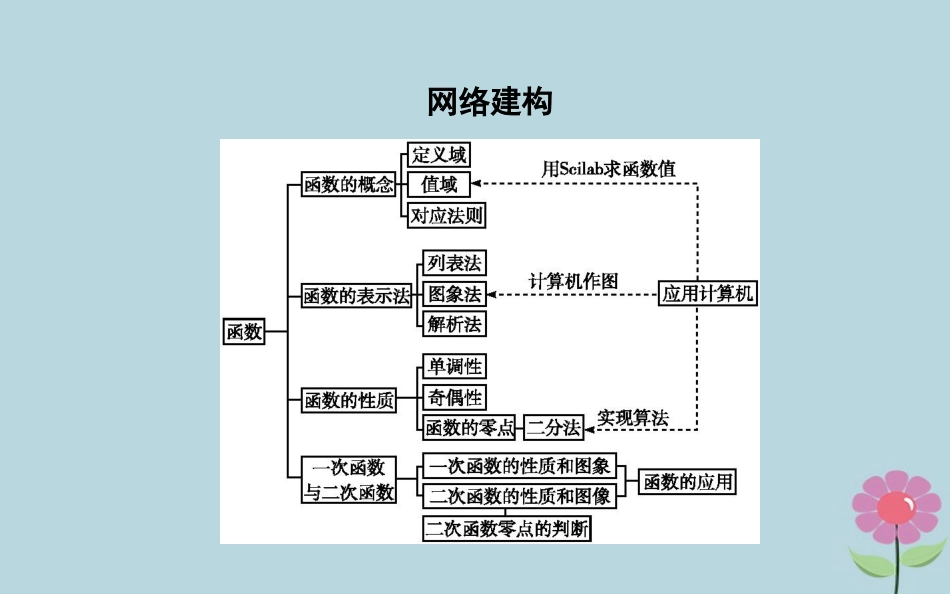
章末总结网络建构名师导学本章要解决的主要问题是:理解函数的概念,表示方法和函数的单调性、奇偶性、零点.通过一次函数、二次函数图象、性质的研究,掌握研究函数的思想方法.解决上述问题的关键是:掌握几种重要的数学方法:待定系数法、换元法、配凑法和二分法.突出数形结合思想、函数与方程思想、分类讨论及化归转化思想的作用,进一步的会应用这些思想方法研究函数.题型探究·素养提升类型一函数的定义域【例1】(1)函数f(x)=1x+12x的定义域为.解析:(1)要使f(x)有意义,须且只需10,20,xx所以1,2,xx所以f(x)的定义域为[-1,2)∪(2,+∞).答案:(1)[-1,2)∪(2,+∞)(2)若关于x的函数f(2x+3)的定义域是{x|-4≤x<5},则关于x的函数f(2x-3)的定义域是.解析:(2)因为f(2x+3)的定义域是{x|-4≤x<5},所以-5≤2x+3<13所以f(2x-3)中2x-3∈[-5,13),所以x∈[-1,8)所以f(2x-3)的定义域是[-1,8).答案:(2)[-1,8)解析:(3)函数f(x2)的定义域为[-1,2],所以0≤x2≤4,在f(2x-1)中令0≤2x-1≤4,所以12≤x≤52,所以f(2x-1)的定义域为15,22.(3)函数f(x2)的定义域为[-1,2],则函数f(2x-1)的定义域为.答案:(3)15,22方法技巧求函数的定义域,对于已知函数解析式求定义域问题,就是使解析式有意义的自变量x的范围;复合函数求定义域要明确中间变量是什么,定义域仍然是解析式中自变量的取值范围.类型二求函数的解析式解:(1)设f(x)=ax2+bx+c(a≠0),因为f(0)=1,所以c=1,f(x+1)-f(x)=2ax+a+b=2x,即22,0,aab得1,1,ab所以f(x)=x2-x+1.【例2】(2018·河北石家庄辛集中学上期中)已知二次函数f(x)满足f(x+1)-f(x)=2x,且f(0)=1.(1)求f(x)的解析式;解:(2)由题意知g(x)=x2+(a-1)x+1,对称轴为x=12a,当12a≤-1即a≥3时,g(x)在[-1,1]上单调递增,g(x)min=g(-1)=3-a;当-1<12a<1即-1
0.所以1212xxxx<0,即f(x1)-f(x2)<0.所以f(x1)0时,令f(x)=0,即1-1x=0,解得x=1>0.所以x=1是函数f(x)的一个零点.(ⅱ)当x≤0时,令f(x)=0,即(a-1)x+1=0.(*)①当a>1时,由(*)得x=11a<0,所以x=11a是函数f(x)的一个零点;(2)求函数f(x)的零点.③当a<1时,由(*)得x=11a>0(不合题意,舍去),综上,当a>1时,函数f(x)的零点是1和11a;当a≤1时,函数f(x)的零点是1.②当a=1时,方程(*)无解;方法技巧由于分段函数在不同定义域上函数的表达式不同,所以处理分段函数的问题,要依据自变量所在的范围选择相应的解析式.类型四函数的图象解:(1)已知函数f(x)=min{(x-1)2,3-x,x+1},如图所示.【例4】(2018·河南濮阳一中高一上期中)用min{a,b,c}表示a,b,c中较小的一个,已知函数f(x)=min{(x-1)2,3-x,x+1}.(1)画出函数f(x)的图象;解:(2)由(1)知f(x)的单调递增区间是(-∞,0),(1,2),单调递减区间是(0,1),(2,+∞).(2)写出函数f(x)的单调区间.方法技巧(1)函数图象是研究函数性质的重要方法,因此涉及非一次函数、二次函数的性质问题,常作出函数图象利用数形结合思想求解.(2)本题中函数的单调递增区间不能写为(-∞,0)∪(1,2),也不能写为(-∞,0)或(1,2).【例5】已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,当a,b∈[-1,1],a+b≠0时,有fafbab>0成立.(1)判断f(x)...