高三数学数列的极限 新课标 人教版 课件VIP免费

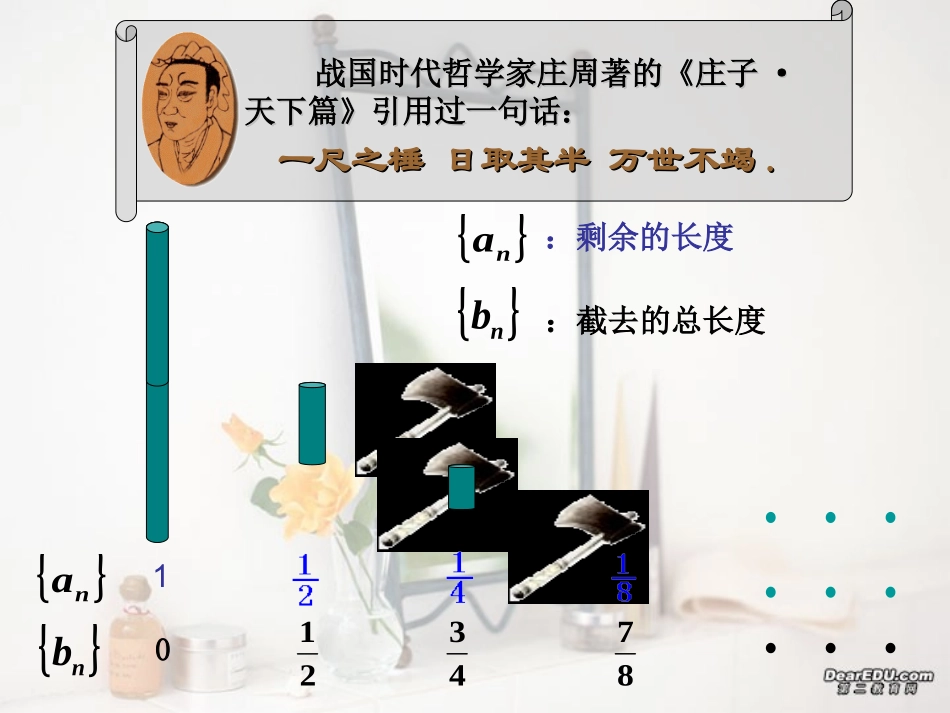
1战国时代哲学家庄周著的《庄子战国时代哲学家庄周著的《庄子··天下篇》引用过一句话：天下篇》引用过一句话：一尺之棰日取其半万世不竭一尺之棰日取其半万世不竭..nanbna：剩余的长度nb：截去的总长度0214387nb0814183218543871x1nanb02143871234nn从1的左侧无限趋近1是什么？的变化趋势分别和的无限增大，随着项数nnban0814183218543871xna从0的右侧无限趋近0表示的点的变化趋势和nnba121n1211n1234………n………1234………n………n1nanb0214387n121n0na1nb1211n1214181121nna无限趋近常数0，无限地接近于00na无限趋近常数1，无限地接近于0nb1nb1214181121n0-13121，，，，n1013101310132（1），，，，，1433221nn（2），，，，２，nn)1(3111（3）分析当n无限增大时，下列数列的项的变化趋势及共同特征:na..............共同特性：不论这些变化趋势如何，随着项数n的无限增大，数列的项无限地趋近于常数ana3递减无限趋近1递增无限趋近0无限趋近摆动n趋向于无穷大aannlim数列极限的描述性定义na一般地，如果当项数无限增大时，无穷数列的项无限地趋近于某个常数，(即无限地接近0),nnaaaan那么就说数列以为极限，或者说naaana是数列的极限na（1）是无穷数列n（2）无限增大时，不是一般地趋近于，而是naa“无限”地趋近于a（3）数值变化趋势：递减的、递增的、摆动的读作“当n趋向于无穷大时，的极限等于a”na或“limit当n趋向于无穷大时等于a”naaannnalim数列是否存在极限若存在极限99.0nna100)(n1nan2nanna)1(aannlim不存在存在存在不存在00－20数列的极限是唯一的有穷数列没有极限099.0n)(lim为常数CCCnaannnalim数列是否存在极限若存在极限aannlimnan1nannann3)1(存在存在不存在00n31n100)(lim)2(是常数CCnnn1lim)1(0C,)3(时当1na0limnna2、给出下列命题：（1）有穷数列没有极限；（2）无穷数列不一定有极限；（3）无穷递减数列一定有数列；（4）无穷递增数列一定没有数列；（5）左右摆动的数列一定没有极限。其中是真命题的序号有3、举出一些存在极限的数列和一些不存在极限的数列（1）、（2）x0yy1、总体密度曲线设想样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线——总体密度曲线数列极限思想的运用割圆求周三国时的刘徽提出的““割圆求周割圆求周””的方法.他把圆周分成三等分、六等分、十二等分、二十四等分、···这样继续分割下去,所得多边形的周长就无限接近于圆的周长.割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体而无所失矣.12345678…项号边数内接多边形周长定量分定量分析析圆的半径21R2412632.5980762113533.0000000000003.1058285412303.132628613281483.139350203047963.1410319508911923.1414524722853843.141557607912……………割圆求周1、数列极限的直观描述性定义），无限地接近（即，无限地趋近于某个常数的项无穷数列无限增大时，一般地，如果当项数0aaaaannnn的极限是数列或者说为极限，以那么就说数列nnaaaaaannlim2、利用定义求数列极限3、常用数列的极限)(lim)2(是常数CCnnn1lim)1(0C,)3(时当1a0limnanAannlim1、若，则下面几个结论中，正确的是（）0的极限是数列一定是递减数列数列一定是递增数列数列一定是递减数列数列AaAaAaAannnnA.B.C.D.012121)(0)1(lim3xxxxxxxnn的取值范围是，则、若A.B.C.D.1101lim2aaaann或、