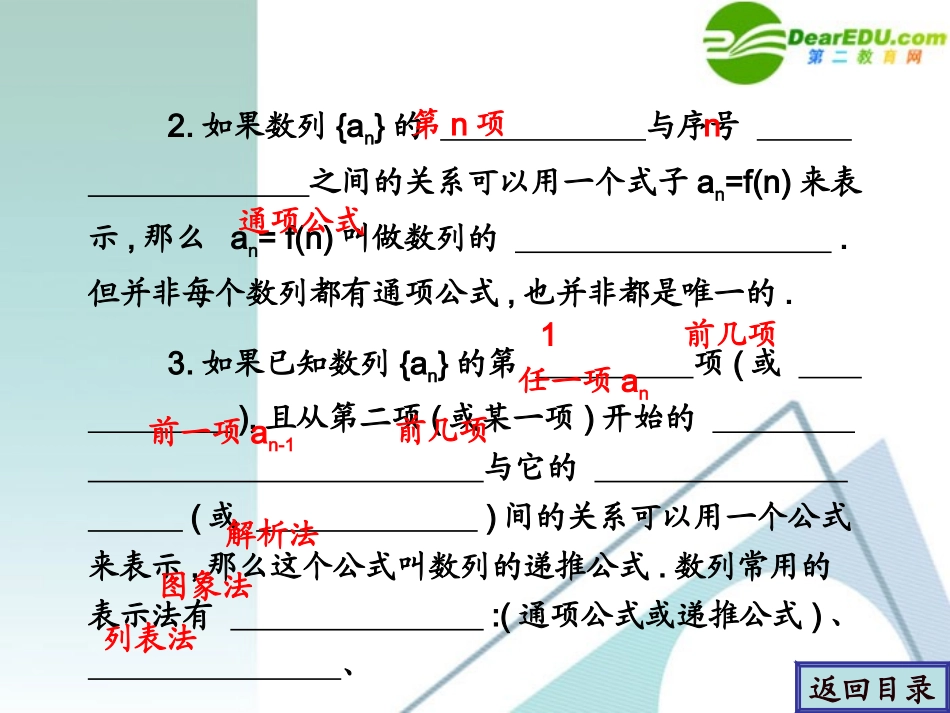
学案学案11数列数列返回目录1.按照叫做数列.数列中的叫做这个数列的项;在函数意义下,数列是定义域为的函数,f(n)是当自变量n从1开始依次取自然数时所对应的一列函数值f(1),f(2),…,f(n),….通常用an代替f(n),故数列的一般形式为:a1,a2,a3,…,an,…,简记为{an},其中an是数列的第项.一定次序排列着的一列数每一个数N*或它的子集n返回目录2.如果数列{an}的与序号之间的关系可以用一个式子an=f(n)来表示,那么an=f(n)叫做数列的.但并非每个数列都有通项公式,也并非都是唯一的.3.如果已知数列{an}的第项(或),且从第二项(或某一项)开始的与它的(或)间的关系可以用一个公式来表示,那么这个公式叫数列的递推公式.数列常用的表示法有:(通项公式或递推公式)、、.第n项n通项公式1前几项任一项an前一项an-1前几项解析法列表法图象法4.数列按项数来分,分为、;按项的增减规律分为、、和.递增数列an+1an;递减数列an+1an;常数列an+1an.递增数列与递减数列通称为.按任何一项的绝对值是否都小于某一正数来分,可分为和.,(n=1),(n≥2).an≥an-1,an≤an-1,an≥an+1.an≤an+1.返回目录Sn-Sn-15.已知Sn,则an=数列{an}中,{{{若an最大,则若an最小,则⇔⇔⇔有穷数列无穷数列递增数列递减数列摆动数列常数列><=单调数列有界数列无界数列S1返回目录写出下面各数列的一个通项公式:(1)3,5,7,9,…;(2)…;(3)-1,,…;(4),…;(5)3,33,333,3333,….考点一由数列前几项求数列通项公式考点一由数列前几项求数列通项公式,3231,1615,87,43,21,53,51,-43,31-,231337,1126,917,-710,1-,32返回目录【分析】【分析】先观察各项的特点,然后归纳出其通项公式,要注意项与项数的关系及项与前后项的关系.【解析】【解析】(1)各项减去1后为正偶数,所以an=2n+1.(2)每一项的分子比分母少1,而分母组成数列21,22,23,24,…,所以an=.(3)奇数项为负,偶数项为正,故通项公式中含因子(-1)n;各项绝对值的分母组成数列1,2,3,4,…;而各项绝对值的分子组成的数列中,奇数项为1,偶数项为3,即奇数项为2-1,偶数项为2+1,nn21-2返回目录所以an=(-1)n·.-(n为正奇数)(n为正偶数).(4)偶数项为负,奇数项为正,故通项公式必含因子(-1)n+1,观察各项绝对值组成的数列,从第3项到第6项可见,分母分别由奇数7,9,11,13组成,而分子则是32+1,42+1,52+1,62+1,按照这样的规律第1,2两项可改写为,,所以an=(-1)n+1.n(-1)+2nn1n3也可写为an={12112++12212-2+×+12n1n2++(5)将数列各项改写为,…,分母都是3,而分子分别是10-1,102-1,103-1,104-1,…,所以an=(10n-1).,39999,3999,399,3931返回目录返回目录【评析】【评析】(1)根据数列的前几项求它的一个通项公式,要注意观察每一项的特点,可使用添项、还原、分割等办法,转化成一些常见数列的通项公式来求.(2)根据数列的前几项写出数列的一个通项公式是不完全归纳法,它蕴含着“从特殊到一般”的思想,由不完全归纳得出的结果是不可靠的,要注意代值检验,对于正负符号变化,可用(-1)n或(-1)n+1来调整.(3)观察、分析问题的特点是最重要的,观察要有目的,观察出项与项数之间的关系、规律,利用我们熟知的一些基本数列(如自然数列、奇偶数列等)建立合理的联想、转换而使问题得到解决.*对应演练**对应演练*根据数列的前几项,写出下列各数列的一个通项公式:(1),,,,…;(2)1,3,6,10,15,…;(3),,-,,…;(4)7,77,777,….5421114722141851613返回目录返回目录(1)注意前四项中有两项的分子均为4,不妨把分子都统一为4,即:,,,,….因而有an=.(2)注意6=2×3,10=2×5,15=3×5,规律还不明显,再把各项同乘以2再除以2,即,…,因而有an=.548411414423n4+265,254,243,232,221×××××2)1n(n+(3)其分母的规律是明显的,关键在于观察分子,分子后三项绝对值递增,且比分母小3.又注意到第三项为负,而第一项的分子也可以写成-(-1),a∴n=(-1)n.(4)把各项除以7,得1,11,111,…,再乘以9,得9,99,999,….a∴n=(10n-1).返回目录97nn23-2返回目录已知下面各数列{an}的前n项和Sn的公式,求{an}的通项公式.(1)Sn=2n2...