高中数学：向量的加法运算及其几何意义课件新人教A版必修4 课件VIP免费

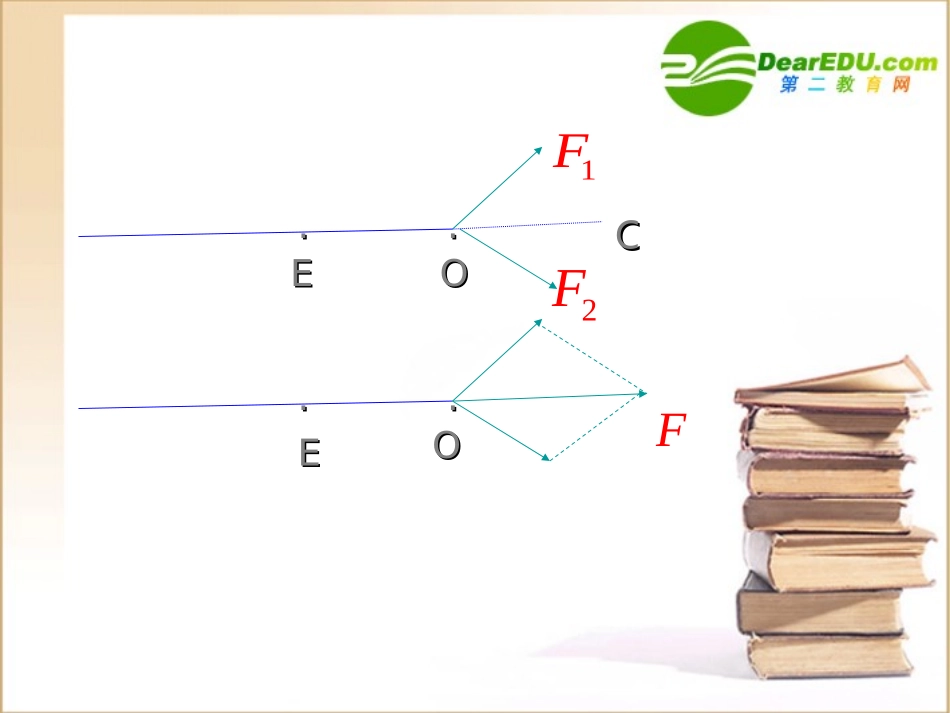
§2.2.1向量加法运算及其几何意义····EEOOCC2F1FEE····OOF实事回放台北香港上海上海上海上海台北香港abAABBCC向量的加法——法则向量加法的三角形法则：首尾相连，首尾连abABBCAC��abc例1如图，已知向量，求作向量,abab3.再以A为起点，做向量abOOAABB1.在平面上任取一点O2.以O为起点，做向量OAa�ABb�则则OBab�向量的加法——练习根据三角形法则，画出下列各题中与的和.abOB(1)abCA向量加法的平行四边形法则起点重合同起点的对角线例1法2,OAaOBb�11．在平面内任取一点．在平面内任取一点OO，作，作2﹒2﹒以以OA﹑OBOA﹑OB为为邻边作平行四边形邻边作平行四边形OACBOACB，连接，连接OC,OC,OCab�abOOAABBCC则则注明：•当两共线向量求和时，选用三角形法则•规定00aaa练习：如图，已知向量，求作向量,ababA(2)Bab(1)ABabCCACab�ACab�思考：•两个向量的和仍是一个向量吗？•它的大小和有何关系？,ab结论：结论：abab,ab(1)研究向量是否满足交换律:abbaabbAD,aAB使,作平行四边形ABCD:作法ABDaDC,bBC则Caabb依作法有：abDCADACbaBCABAC向量加法的运算律(2)研究向量是否满足结合律:)()(cbacbacbabacbBAaCbcD由此可推广到多个向量加法运算可按照任意的次序与任意的组合进行bcaddcbacadbdcba)]([)()()()(例子练习•如图，在四边形ABCD中，证明ABCD证：证：CBADBACBADBACBBAADCBBDCD�����CBADBACD�例2如图，一艘船从长江南岸A点出发，以km/h的速度向垂直于对岸的方向行驶，同时江水速度为向东5km/h.（1）试用向量表示江水速度，船速及船实际航行的速度（保留两个有效数字）（2）求船实际航行的速度大小与方向（用与江水速度间的夹角表示）。53ABCD解：（1）如图所示，表示船速，表示水速，以AD﹑AB为邻边作平行四边形ABCD，则表示船实际航行速度。AC�AD�（（22）在中）在中RtABC22ACABBC�2253510010tan3CAB60CABAB�因为因为所以所以答：船实际航行速度的大小为答：船实际航行速度的大小为10km/h,10km/h,方向与水方向与水的流速间的夹角为。的流速间的夹角为。60)cb(ac)ba(abba作业：•学案中的练习题