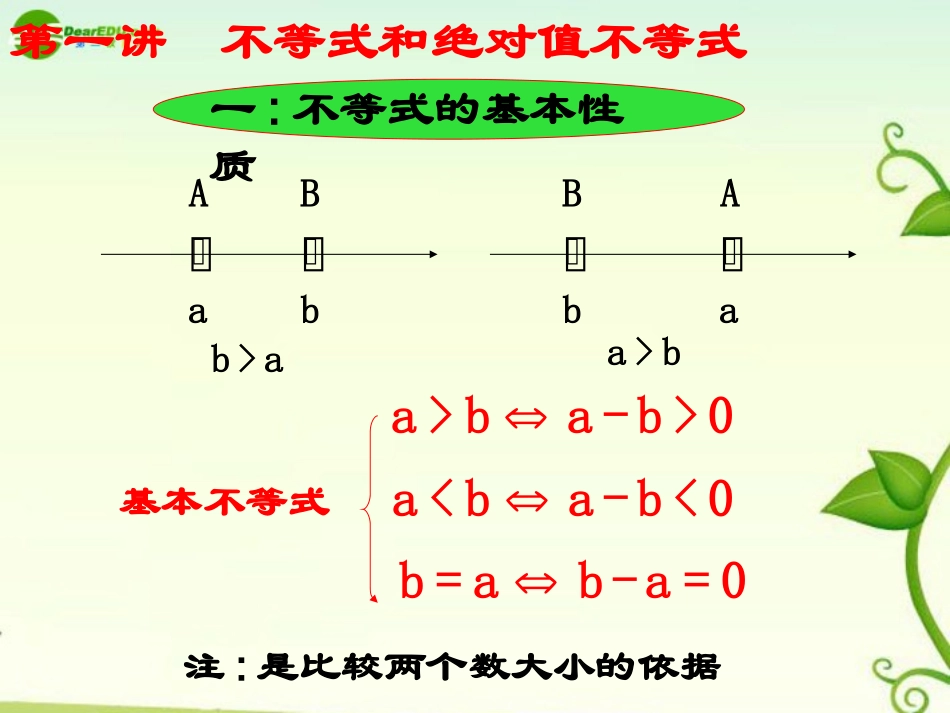
选修4-5不等式选讲本专题知识结构第一讲不等式和绝对值不等式第三讲柯西不等式与排序不等式第四讲数学归纳法证明不等式第二讲证明不等式的基本方法不等式选讲AaBbAaBbb>aa>baba-b>0b=ab-a=0基本不等式注:是比较两个数大小的依据一:不等式的基本性质第一讲不等式和绝对值不等式比较法的基本步骤:比较法的基本步骤:1.作差(或作商)2.变形3.定号定号((与与00比较或与比较或与11比较比较).).例1:比较(x+1)(x+2)和(x-3)(x+6)的大小。解:因为(x+1)(x+2)-(x-3)(x+6)=x2+3x+2-(x2+3x-18)=20>0,所以(x+1)(x+2)>(x-3)(x+6)①、对称性:传递性:_________②、,a+c>b+c③、a>b,,那么ac>bc;a>b,,那么ac<bc④、a>b>0,那么,ac>bd⑤、a>b>0,那么an>bn.(条件)⑥、a>b>0那么(条件)nnbaabbacacbba,Rcba,0c0c0dc2,nNn2,nNn(可加性)(可乘性)(乘法法则)(乘方性)(开方性)一:不等式的性质2例cbdadcba求证已知,0,0011,01,0,0,0:cddccdcddccddc证明,0,0,011cadaacd又①②由①②可得cbdacbda,0,0,01,0cbcacba又课堂练习:1.判断下列命题是否正确:(1)cabcba,()(2)bcacba()(3)22bcacba()(4)bdacdcba,()(5)bacbca22()(6)baba22()(7)22baba()(8)22baba()(9)dbcadcba0,0()2.设A=1+2x4,B=2x3+x2,xR∈且x≠1,比较A,B的大小.×√××√××√×解: A-B=1+2x4-(2x3+x2)=432(22)(1)xxx=32(1)(1)(1)xxxx=3(1)(21)xxx=2(1)(1)(221)xxxx=2211(1)2()022xx∴A>B3.若a、b、x、y∈R,则是成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件()()0xyabxaybxaybC5.已知f(x)=ax2+c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围。4.对于实数a、b、c,判断下列命题的真假:(1)若c>a>b>0,则(2)若a>b,,则a>0,b<0。abcacb11ab(真命题)(真命题)f(3)的取值范围是[-1,20]二:基本不等式22如果a,b∈R,那么a+b≥2ab,当且仅当a=b时等定理1:号成立。aabbb几何解释(基本不等式)a+b如果a,b0,那么≥ab,2当且仅当a=b时等定理2:号成立。三:基本不等式算术平均数几何平均数几何解释OabDabACB两个正数的算术平均不小于它们的几何平均。注:一正、二定、三等。例3求证:(1)在所有周长相同的矩形中,正方形的面积最大;(2)在所有面积相同的矩形中,正方形的周长最短.定理:设,,xyz都是正数,则有⑴若xyS(定值),则当xy时,xy有最小值2.s⑵若xyp(定值),则当xy时,xy有最大值2.4p例:某居民小区要建一做八边形的休闲场所,它的主体造型平面图是由两个相同的矩形ABCD和EFGH构成的面积为200平方米的十字型地域.计划在正方形MNPQ上建一座花坛,造价为每平方米4300元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价没平方米210元,再在四个空角(图中四个三角形)上铺草坪,每平方米造价80元.(1)设总造价为S元,AD长x为米,试建立S关于x的函数关系式;(2)当为何值时S最小,并求出这个最小值.QDBCFAEHGPMN解:设AM=y米22200-x从而4xy+x=200y=4x22于是S=4200x+210×4xy+80×2y0