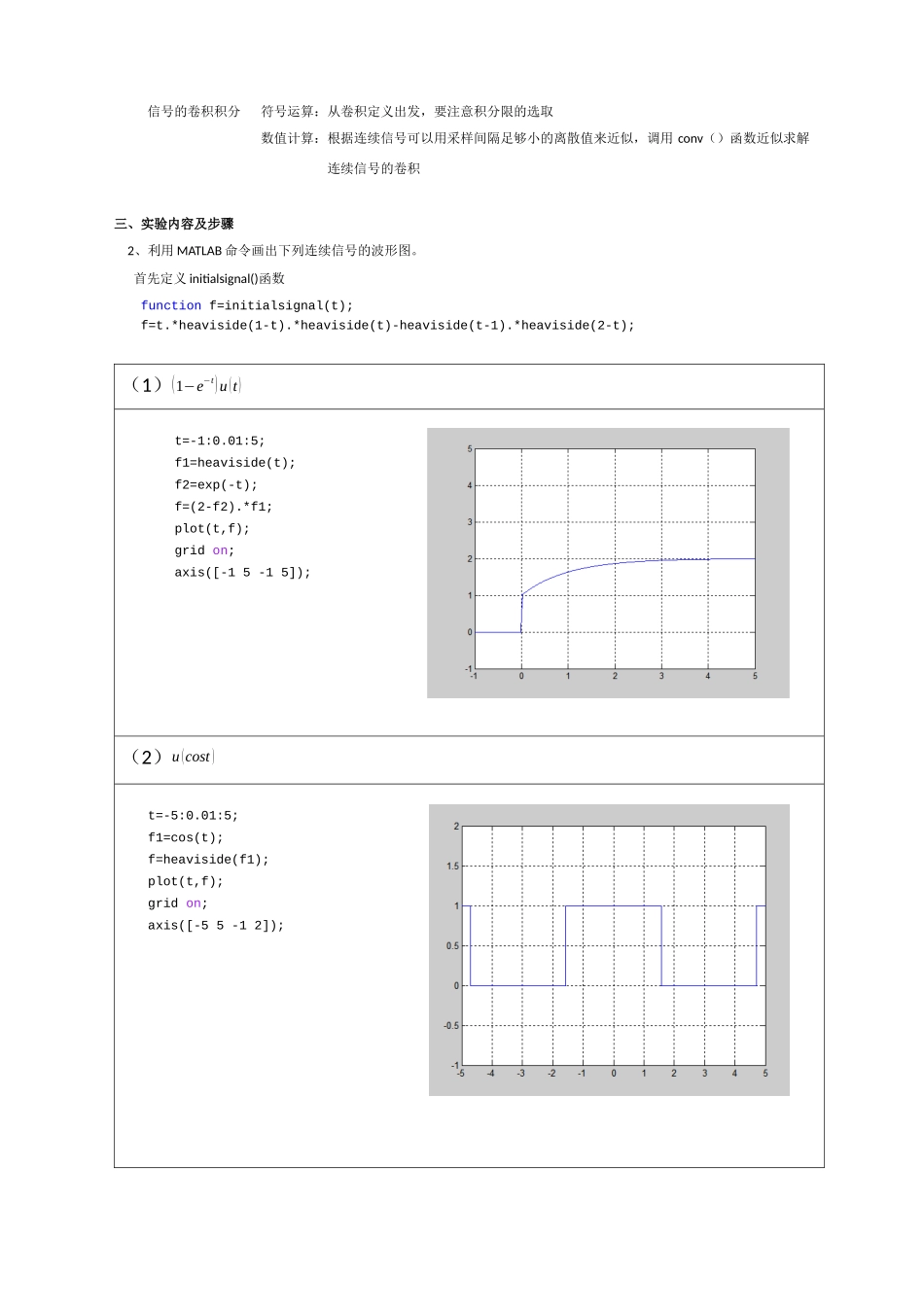
课程实验报告课程名称:信号与系统实验项目名称:实验一专业班级:通信工程1302班姓名:吴绍启学号:201308030204指导教师:胡红平完成时间:2015年5月29日实验一连续信号的时域描述与运算一、实验目的1.通过绘制典型信号的波形,了解这些信号的基本特征。2.通过绘制信号运算结果的波形,了解这些信号运算对信号所起的作用。二、实验原理1、如果一个信号在连续时间范围内有定义,则称该信号为连续时间信号,简称为连续信号。从严格意义上来讲,MATLAB数值计算方法并不能处理连续信号,但是可利用连续信号在等时间间隔点的采样值来近似表示覅连续信号,即当采样间隔足够小时,这些离散采样值能够被MATLAB处理,并且能较好的近似表示连续信号。一种方法是向量表示法,定义两个行向量f和t,当时间间隔取得足够小时,就可以得到f(t)的近似波形。在这种方法中,主要的绘图函数是plot(t,y)另一种方法是符号运算表示法。如果信号可以用一个符号表达式来表示,则可用ezplot命令绘制出信号的波形。可以用sym()来产生符号表达式2、常用连续信号的MATLAB表示单位阶跃信号:U(t),MATLAB中用heaviside()表示单位冲激信号:δ(t),MATLAB中用Dirac()表示实指数信号:f=A.*exp(a*t)3、连续信号的基本运算信号相加和相乘f1+f2f1.*f2信号微分和积分微分:diff(function,’variable’,n);n为求导的阶数积分:int(function,’variable’,a,b);a,b为积分上下限信号平移和反转平移和反转并不会改变一个信号的面积或能量信号的尺度变换对信号在时间轴上的压缩、扩展信号的奇偶分量奇分量:1/2[f(t)-f(-t)]偶分量:1/2[f(t)+f(-t)]信号的卷积积分符号运算:从卷积定义出发,要注意积分限的选取数值计算:根据连续信号可以用采样间隔足够小的离散值来近似,调用conv()函数近似求解连续信号的卷积三、实验内容及步骤2、利用MATLAB命令画出下列连续信号的波形图。首先定义initialsignal()函数functionf=initialsignal(t);f=t.*heaviside(1-t).*heaviside(t)-heaviside(t-1).*heaviside(2-t);(1)(1−e−t)u(t)t=-1:0.01:5;f1=heaviside(t);f2=exp(-t);f=(2-f2).*f1;plot(t,f);gridon;axis([-15-15]);(2)u(cost)t=-5:0.01:5;f1=cos(t);f=heaviside(f1);plot(t,f);gridon;axis([-55-12]);(3)产生幅度为1、周期为1、占空比为0.5的周期矩形信号。t=-3:0.001:3;f1=square(2*pi*t,50);f=heaviside(f1);plot(t,f);gridon;axis([-22-0.51.5]);3、已知f(t)的波形如图所示,作出:a.f(t)+f(t)、f(t)·f(t)b.f(t)的微分、f(t)的积分c.f(3−4t)、f(1−t/1.5)的波形d.并作出f(t)的奇偶分量。t=0:0.001:3;f=t.*heaviside(1-t).*heaviside(t)-heaviside(t-1).*heaviside(2-t);f1=f+f;f2=f.*f;figure(1);subplot(121);plot(t,f1);gridon;axis([03-2.52.5]);title('f(t)+f(t)');subplot(122);plot(t,f2);gridon;axis([03-2.52.5]);title('f(t)*f(t)');t=-5:0.01:5;f=initialsignal(t);f1=initialsignal(3-4*t);f2=initialsignal(1-t/1.5);f4=initialsignal(-t);figure(1);plot(t,f1);gridon;axis([-11-22]);title('f(3-4*t)');figure(2);plot(t,f2);gridon;axis([-22-22]);title('f(1-t/1.5)');T=0.01;t=0:T:5;f3=T*conv(f,f1);tmin=-10;tmax=10;t1=tmin:0.01:tmax;figure(3);plot(t1,f3);gridon;title('f(t)*f(3-4t)')fe=0.5*(f+f4);fo=0.5*(f-f4);figure(4);subplot(121);t1=-5:0.01:5;plot(t1,fe);gridon;title('偶分量');subplot(122);plot(t1,fo);gridon;title('奇分量');三、思考题1、讨论f(t+t0)与f(−t+t0)的平移方向是否相同?为什么不相同,f(−t+t0)相当于f(−(t−t0)),即f(t)先对t反转再向右平移t0,而f(t+t0)由f(t)左平移t0得到,所以两者平移方向不同。2、将信号f(t)变成f(−2t+4)共有多少种方法,请列举出来。a.先将f(t)时间尺度压缩为原来的2倍,变为f(2t),再对时间进行反转f(−2t),再向右平移2个单位,变为f(−2t+4)。b.先将f(t)左移4个单位变为f(t+4),再将时间压缩为原来的2倍,变为f(2t+4),再将信号进行反折,变为f(−2t+4)。