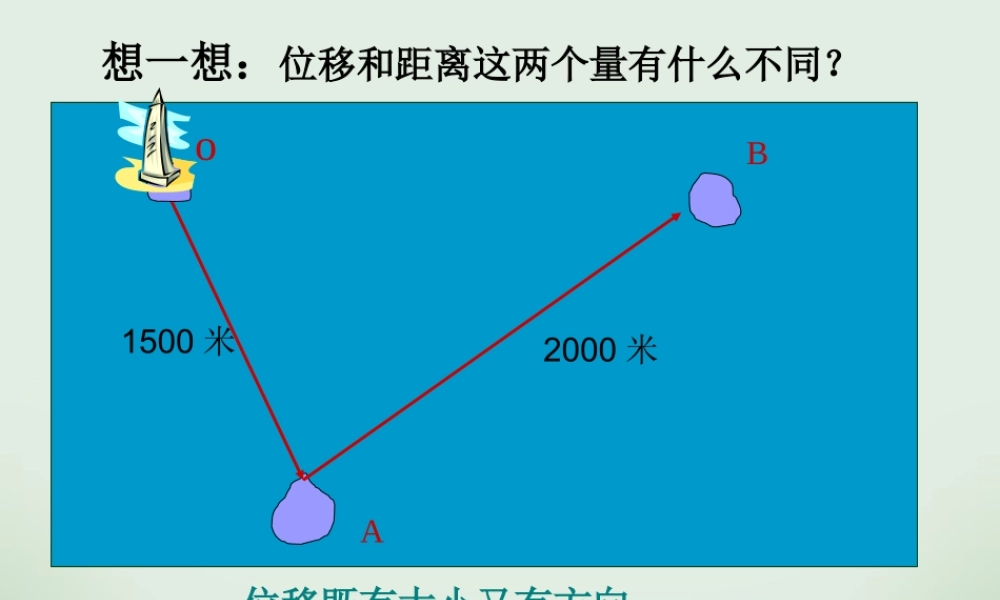
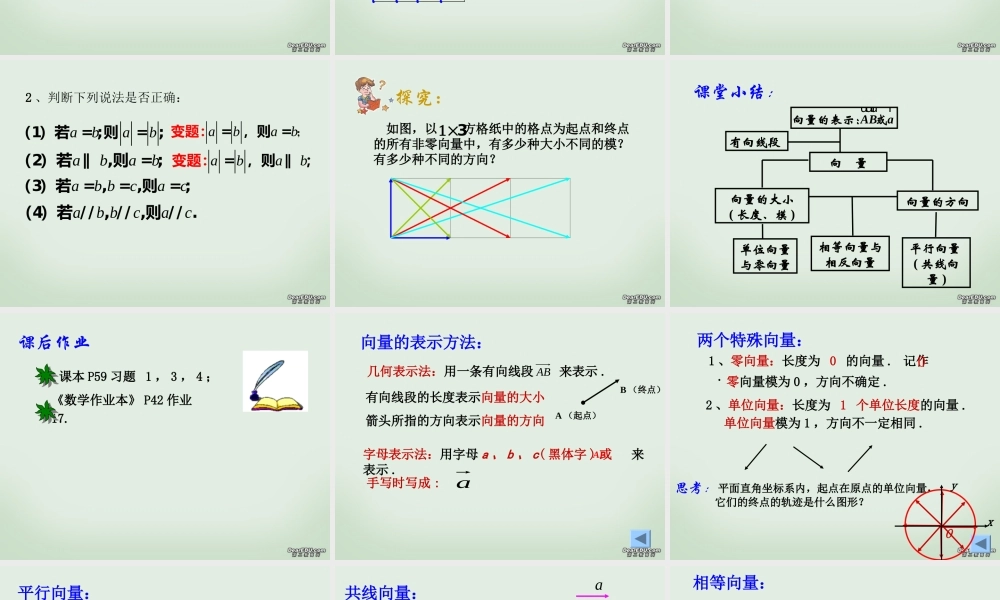
想一想:位移和距离这两个量有什么不同?oBA2000 米1500 米位移既有大小又有方向距离只有大小没有方向向量的概念及表示生活中有向量 生活中用向量阅读课本 P57 - 58 完成下列问题 :1. 什么是向量 ?2. 怎么表示向量?3. 什么是向量的模 ?4. 有哪些特殊向量?5. 向量间有什么特殊关系?既有大小又有方向的量称为向量 .1 )几何表示;2 )字母表示;指向量的长度AB�记作:||零向量单位向量平行向量共线向量相等向量相反向量�(1)和解.BC OA�(2).BC�(3)虽然∥,且=,但它们方向相反,故这两个向量并不相等.OABCOABCOFEFEOABC���例1:已知 为正六边形的中心,在图中所标出的向量中:(1)试找出与共线的向量;(2)确定与相等的向量;(3) 与相等吗?若不相等, 则它们之间有什么关系?ABCDEFABCDEFOABCDEFO变 1: 以图中 A,B,C,D,E,F,O 七点中的任一点为始点,与始点不同的另一点为终点的所有向量中,与向量 相等的向量有几个?OAuur变 2 : 的相反向量有几个?OAuur3个4个3 4AB�AB�AB�AB� 例 2 :在图中的方格纸中有一个向量 , 分别以图中的格点为起点和终点作向量,其中与 相等的向量有多少个?与 长度相等的共线向量 有多少个?(除外)7AB�共有 个向量与相等(1)(2)15AB�共有个向量与共线AB●●●●●●● 1 、下列说法正确的是( )OABCAO BO CO�,、 、;C.设 是正的中心则向量是模相等的向量;A.共线的向量,若起点不同,则终点一定不同ABCDABCD�D.向量与是共线向量,则 、 、 、四点必在一直线上.abab;B.若 和 都是单位向量,则 =课堂练习C2 、判断下列说法是否正确: ab bcac(3)若 = , = ,则 = ;ab bcac(4)若 // , // ,则 // .abab= ,则变∥题:;abab(2)若 ∥,则 = ;abab;= ,则 =变题:abab(1)若 = ;则= ;探究: 如图,以 方格纸中的格点为起点和终点的所有非零向量中,有多少种大小不同的模?有多少种不同的方向?3相等向量与相反向量课堂小结:单位向量与零向量向 量ABauuurr向量的表示: 或向量的大小( 长度、模 )向量的方向有向线段平行向...