高三数学总复习导与练 第十三篇第3节配套课件(教师用) 理 课件VIP免费

第 3 节 柯西不等式柯西不等式 (1)二维形式：若 a，b，c，d 都是实数，则(a2＋b2)(c2＋d2)≥(ac＋bd)2，当且仅当 ad＝bc 时，等号成立． (2)三维形式：若 a1，a2，a3，b1，b2，b3 都是实数，则(a12＋a22＋a32)(b12＋b22＋b32)≥(a1b1＋a2b2＋a3b3)2，当且仅当 b1＝b2＝b3＝0 或存在一个实数 k，使得 a1＝kb1，a2＝kb2，a3＝kb3时，等号成立． 质疑探究：柯西不等式的外在形式如何记忆？ 提示：可以理解为“方和积≥积和方”． 2．已知 x＋y＝1，那么 2x2＋3y2 的最小值是( B ) (A)56 (B)65 (C)2536 (D)3625 解析：(2x2＋3y2)[( 12)2＋( 13)2]≥( 2x× 12＋ 3y× 13)2＝(x＋y)2＝1. 当且仅当 2x＝3y，即 x＝35，y＝25时等号成立． ∴56(2x2＋3y2)≥1，∴2x2＋3y2≥65.故应选 B. 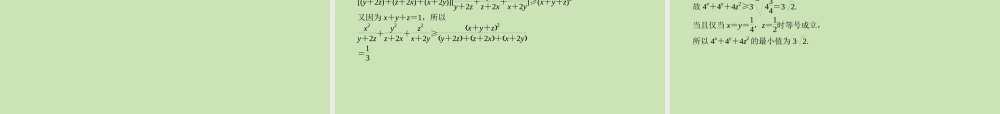1．设 a，b∈R＋，P＝a3＋b3，Q＝a2b＋ab2，则 P、Q 间的大小关系是( B ) (A)P>Q (B)P≥Q (C)P0，b>0 且 a≠b，P＝a2b ＋b2a ，Q＝a＋b，则( A ) (A)P>Q (B)P≥Q (C)Pb>0，则ab>ba，由顺序和≥反序和，则 a·ab＋b·ba≥a·ba＋b·ab＝a＋b.又 a≠b，∴a2b ＋b2a >a＋b，故选 A. 4．已知 x，y，z∈R＋，且 x＋y＋z＝4，则x＋2 y＋3z的最大值为________． 解析： ( x＋2 y＋ 3z)2＝(1× x＋2× y＋ 3× z)2 ≤[12＋22＋( 3)2][(x)2＋( y)2＋(z)2] ＝8×(x＋y＋z)＝32. ∴x＋2 y＋3z≤4 2(当x1＝y4＝z3时，即 x＝12，y＝2，z＝32时取等号)． 答案：4 2 (对应学生用书第 198 页) 利用柯西不等式证明不等式 【例 1】 设 a，b，c 为正数，且 a＋b＋c＝1，求证：1a＋1b＋1c≥9. 思路点拨：结合已知条件对所证不等式变形构造柯西不等式的形式证明． 证明：构造两组数：a， b，c； 1a， 1b， 1c.因此根据柯西不等式有[(a)2＋(b)2＋(c)2][( 1a)2＋( 1b)2＋( 1c)2] ≥( a× 1a＋b× 1b＋c× 1c)2. 即(a＋b＋c)(1a＋1b＋1c)≥32＝9. (当且仅当a1a＝ b1b＝ c1c，即 a＝b＝c 时取等号)． 又 a＋b＋c＝1，所以1a＋1b＋1c≥9. 使用柯西不等式时，关键是将已知条件通过配凑，变为符合柯西不等式条件的式子． 变式探究 11：设 a，b，c 为正数，求证：a2b ＋b2c ＋c2a ≥a＋b＋c. 证明：由柯西不等式知[(...