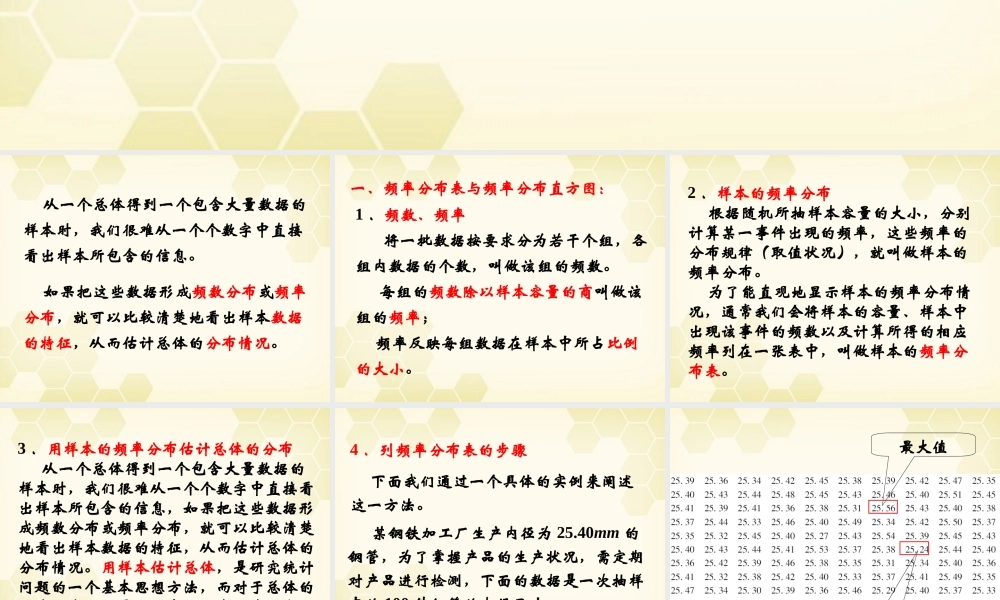
2.2.1 用样本的频率分布估计总体的分布 ( 一 ) 从一个总体得到一个包含大量数据的样本时,我们很难从一个个数字中直接看出样本所包含的信息。 如果把这些数据形成频数分布或频率分布,就可以比较清楚地看出样本数据的特征,从而估计总体的分布情况。 一、频率分布表与频率分布直方图: 1 .频数、频率 将一批数据按要求分为若干个组,各组内数据的个数,叫做该组的频数。 每组的频数除以样本容量的商叫做该组的频率; 频率反映每组数据在样本中所占比例的大小。 2 .样本的频率分布 根据随机所抽样本容量的大小,分别计算某一事件出现的频率,这些频率的分布规律(取值状况),就叫做样本的频率分布。 为了能直观地显示样本的频率分布情况,通常我们会将样本的容量、样本中出现该事件的频数以及计算所得的相应频率列在一张表中,叫做样本的频率分布表。 3 .用样本的频率分布估计总体的分布 从一个总体得到一个包含大量数据的样本时,我们很难从一个个数字中直接看出样本所包含的信息,如果把这些数据形成频数分布或频率分布,就可以比较清楚地看出样本数据的特征,从而估计总体的分布情况。用样本估计总体,是研究统计问题的一个基本思想方法,而对于总体的分布,我们总是用样本的频率分布对它进行估计。 4 .列频率分布表的步骤 下面我们通过一个具体的实例来阐述这一方法。 某钢铁加工厂生产内径为 25.40mm 的钢管,为了掌握产品的生产状况,需定期对产品进行检测,下面的数据是一次抽样中的 100 件钢管的内径尺寸: 最大值最小值 列频率分布表的方法步骤:① 求极差(也称全距,即一组数据中最大值与最小值的差): 计算极差时,需要找出这组数据的最大值和最小值,当数据很多时,可借助如下算法(最大值):S1 把这 100 个数据命名为 A(1) 、 A(2) 、A(3) 、……、 A(100) ;S2 设变量 x=A(1) ;S3 把 A(i) (i=2 , 3 ,……, 100) 逐个与x 比较,如果 A(i)>x ,则 x=A(i) ; 运用上面的算法得出这组样本数据的最大值是 25.56 ,用类似的算法可以得出最小值是 25.24 它们的差为 25.56 - 25.24= 0.32 ,所以极差等于 0.32mm.② 决定组距与组数 那么组数 = ——— =10.67, 于是分成 11 组。极差组距 样本数据有 100 个,由上面算得极差为0.32 ,取组距为 0.03 , 注意:为方便起见,组距的选择应力求“取整”,如果极差不利于分组( 如不能被组数整除)...