高一数学 平面向量的数量积 课件VIP免费

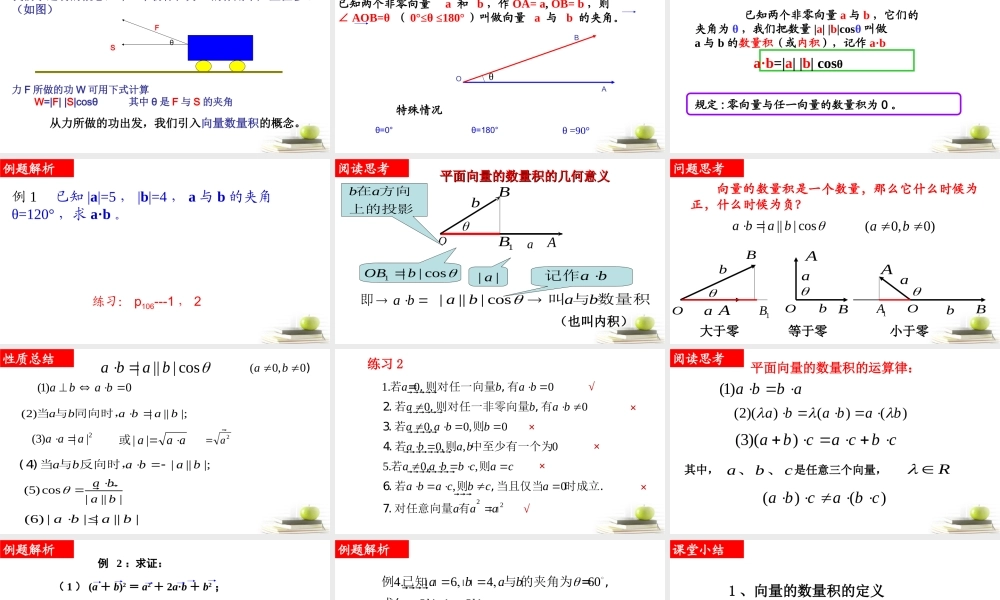
我们学过功的概念，即一个物体在力 F 的作用下产生位移 s（如图）θFS力 F 所做的功 W 可用下式计算 W=|F| |S|cosθ 其中 θ 是 F 与 S 的夹角 从力所做的功出发，我们引入向量数量积的概念。问题思考θ=180°θ =90°向量的夹角已知两个非零向量 a 和 b ，作 OA= a, OB= b ，则∠ AOB=θ （ 0°≤θ ≤180° ）叫做向量 a 与 b 的夹角。θ=0°特殊情况OBAθ阅读思考 已知两个非零向量 a 与 b ，它们的夹角为 θ ，我们把数量 |a| |b|cosθ 叫做a 与 b 的数量积（或内积），记作 a·b a·b=|a| |b| cosθ规定 : 零向量与任一向量的数量积为 0 。阅读思考向量数量积的义例 1 已知 |a|=5 ， |b|=4 ， a 与 b 的夹角θ=120° ，求 a·b 。练习： p106---1 ， 2例题解析aOAbB1B1|| cosOBb ba在 方向上的投影|||| cosabab 叫 与 数量积a b 即a b记作（也叫内积）||a阅读思考平面向量的数量积的几何意义平面向量的数量积的几何意义 向量的数量积是一个数量，那么它什么时候为正，什么时候为负？|||| cosa ba b OabBAOabBAabABO1B1A大于零等于零小于零(0,0)ab问题思考(1)0aba b  (2)||||;aba bab 当 与 同向时，||||;aba bab (4)当 与 反向时，2(3)||a aa aaa||或2a(5)cos||||a bab(6) || ||||a bab(0,0ab)|||| cosa ba b 性质总结√××××√×练习 2221.00000,0,00,,05.0,,0aba baba baa bba ba baa bb caca ba cbcaaaa         若 =, 则对任一向量 , 有2. 若, 则对任一非零向量 , 有3. 若则4. 若则中至少有一个为若,则6. 若则, 当且仅当时成立.7. 对任意向量 有平面向量的数量积的运算律：其中，cba、、是任意三个向量，R()()a bcab c  (1)a bb a  (2)()()()aba bab  (3)()abca cb c   阅读思考例 2 ：...