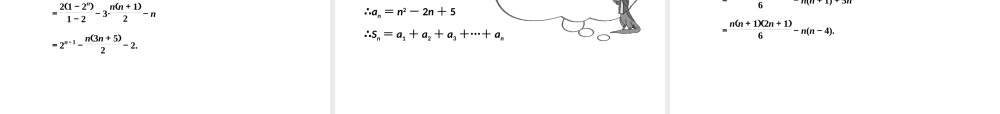高考数学 第五章第四节 数列求和课件 新人教A版 课件VIP免费

1．数列{an}的前 n 项和为 Sn，若 an＝1nn＋1，则 S5 等于 ( ) A．1 B.56 C.16 D. 130 解析： an＝1nn＋1＝1n－ 1n＋1， ∴S5＝a1＋a2＋a3＋a4＋a5＝(1－12)＋(12－13)＋(13－14)＋(14－15)＋ (15－16)＝1－16＝56. 答案： B2．已知数列{ann }的前 n 项和为 Sn，且满足 a1＝1，an＝an－1＋n， 则 Sn 等于 ( ) A.nn＋32 B.nn＋34 C.nn＋12 D.nn＋14 解析： an ＝ an － 1 ＋ n ，即 an － an － 1 ＝ n∴a2 － a1 ＝ 2 ， a3 － a2 ＝ 3 ，…， an － an － 1 ＝ n∴(a2 － a1) ＋ (a3 － a2) ＋ (a4 － a3) ＋…＋ (an － an－ 1)＝ 2 ＋ 3 ＋ 4 ＋…＋ n即 an － a1 ＝ 2 ＋ 3 ＋ 4 ＋…＋ n又 a1 ＝ 1∴an＝1＋2＋3＋4＋…＋n＝nn＋12， ∴ann ＝n＋12 .∴Sn＝a1＋a22 ＋a33 ＋…＋ann ＝12[2＋3＋4＋…＋(n＋1)] ＝nn＋34. 答案： B解析：S2012＝－1＋2－3＋4－5＋…＋2008－2009＋2010－2011＋2012＝(2－1)＋(4－3)＋(6－5)＋…＋(2010－2009)＋(2012－2011)＝10061 111        个＝1006. 答案： D3 ．数列 {( － 1)n·n} 的前 2012 项的和 S2012 为 ( )A ．－ 2012 B ．－ 1006C ． 2012 D ． 10064 ．已知数列 {an} 的前 n 项和为 Sn 且 an ＝ n·2n ，则 Sn ＝ ______.解析： an＝n·2n ∴Sn＝1·21＋2·22＋3·23＋…＋n·2n ① ∴2Sn＝1·22＋2·23＋…＋(n－1)·2n＋n·2n＋1 ② ①－②得－Sn＝2＋22＋23＋…＋2n－n·2n＋1 ＝21－2n1－2 －n·2n＋1 ＝ 2n ＋ 1 － 2 － n·2n ＋ 1＝ (1 － n)2n ＋ 1 － 2∴Sn ＝ 2n ＋ 1(n － 1) ＋ 2.答案： (n － 1)·2n ＋ 1 ＋ 25．数列 1,412，714，1018，…前 10 项的和为________． 解析：1＋412＋714＋1018＋…＋28 1512 ＝(1＋4＋7＋…＋28)＋(12＋14＋18＋…＋ 1512) ＝145511512. 答案：145511512 数列求和的常用方法．1 ．公式法(1) 如果一个数列是等差数列或等比数列，则求和时直接利用等差、等比数列的前 n 项和公式，注意等比数列公比 q 的取值情况要分 q ＝ 1 或 q≠1.(2)一些常见数列的前 n 项和公式： ①1＋2＋3＋4＋…＋n＝ ②1＋3＋5＋7＋…＋2n－1＝ ③2＋4＋6＋8...