高中数学：12(三角函数的诱导公式 2)课件(苏教版必修4)VIP免费

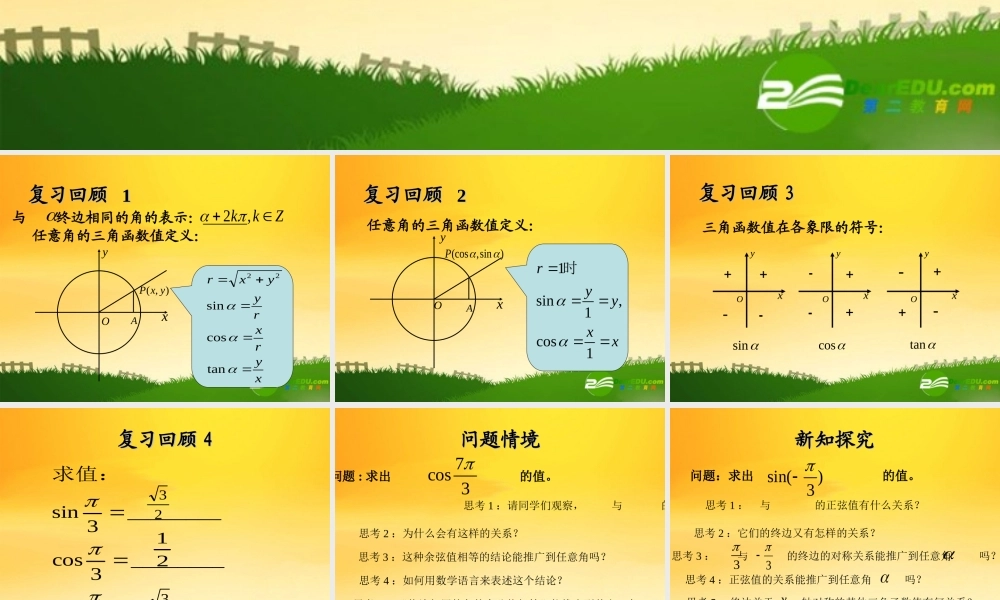
三角函数的三角函数的复习回顾复习回顾 11任意角的三角函数值定义：),(yxPAOxyrxryyxrtancossin22xy与 终边相同的角的表示： Zkk,2 复习回顾复习回顾 22任意角的三角函数值定义：)sin,(cosPAOxxyyr1cos,1sin1时xy复习回顾复习回顾 3 3 三角函数值在各象限的符号：OxyOxyOxysincostan复习回顾复习回顾 44________3tan________3cos________3sin求值：23213问题情境问题情境37cos 问题 : 求出 的值。思考 1 ：请同学们观察， 与 的余弦值有什么关系？337思考 2 ：为什么会有这样的关系？思考 3 ：这种余弦值相等的结论能推广到任意角吗？思考 4 ：如何用数学语言来表述这个结论？思考 5 ：“终边相同的角的余弦值相等”能推广到其它三角 函数值吗？新知探究新知探究问题：求出 的值。)3sin( 思考 1 ： 与 的正弦值有什么关系？ 33思考 2 ：它们的终边又有怎样的关系？思考 4 ：正弦值的关系能推广到任意角 吗？思考 5 ：终边关于 轴对称的其他三角函数值有何关系？x思考 3 ： 与 的终边的对称关系能推广到任意角 吗？33新知探究新知探究思考 6 ：正切值的关系如何得出？tancossin)cos()sin()tan(转化化归思想合作探究合作探究活动 1 、请同学们研究 与 之间的三角函数值的关系。 活动 2 、请同学们研究 与 之间的三角函数值的关系。 合作探究合作探究思考：公式四可以由公式二、三推出吗？sin)sin())(sin()sin(公式二、三、四可以互推转化化归知识运用知识运用 角度函数名sincostan661366567例 5 、请同学们完成下列表格：212333212333212333212333212333知识运用知识运用思考 1 ：观察表格的每一行，同学们看看什么不完全相同，什么完全相同？绝对值相等，符号不完全相同。思考 2 ：符号由什么确定？角的终边所在象限。思考 3 ：若我们将诱导公式中的角 视为锐角，我们可以发现什么规律？ 作锐角，函数名不变，符号看象限作锐角，函数名不变，符号看象限知识运用知识运用例 6 、求值：)316sin(知识运用知识运用思考：为什么把这个公式称为诱导公式？思考：为什么把这个公式称为诱导公式？因为诱导公式的作用在于把求任意角的三角函数值...