高中数学 311(两角差的余弦公式)课件 新人教A版必修4 课件VIP免费

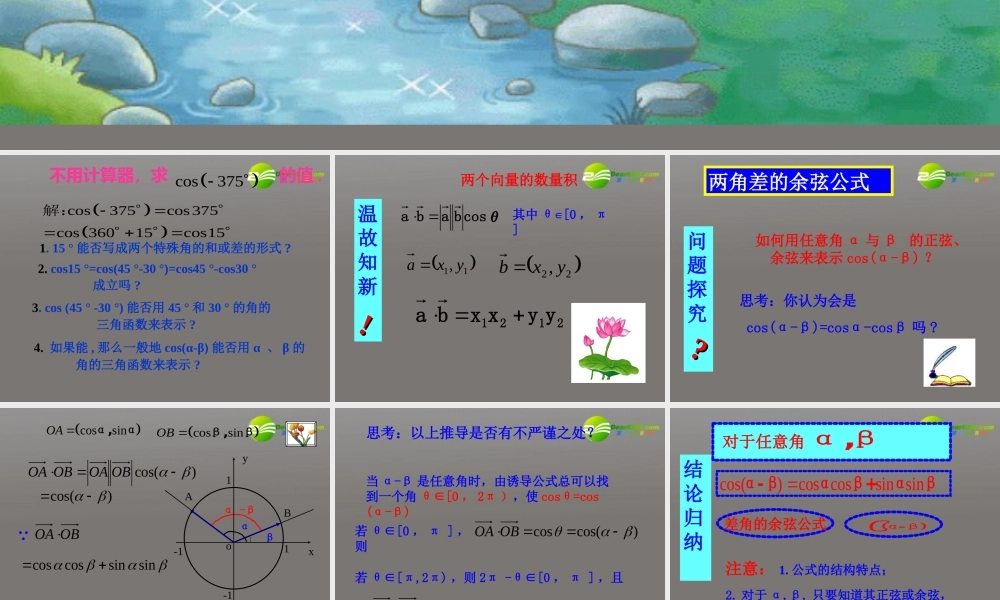
3.1.1 两角差的余弦公式 不用计算器，求 的值 . 1. 15 ° 能否写成两个特殊角的和或差的形式 ? 2. cos15 °=cos(45 °-30 °)=cos45 °-cos30 ° 成立吗 ? 3. cos (45 ° -30 °) 能否用 45 ° 和 30 ° 的角的 三角函数来表示 ? 4. 如果能 , 那么一般地 cos(α-β) 能否用 α 、 β 的 角的三角函数来表示 ?cos375cos375cos375cos 36015cos15 解： cosθbaba其中 θ∈[0 ， π ]2121yyxxba11, yxa 22, yxb 两个向量的数量积温故知新!! 两角差的余弦公式问题探究??如何用任意角 α 与 β 的正弦、余弦来表示 cos(α-β) ？思考：你认为会是cos(α-β)=cosα-cosβ 吗 ? -111-1α -β BAyxoβαcossinOA �α,αcossinOB �β,β)cos( OBOAOBOA)cos( OBOAsinsincoscos∵ ∴ cos(α-β)=cosαcosβ+sinαsinβ 思考：以上推导是否有不严谨之处？当 α-β 是任意角时，由诱导公式总可以找到一个角 θ∈[0 ， 2π ），使 cosθ=cos(α-β)若 θ∈[0 ， π ] ，则)cos(cosOBOA若 θ∈[π,2π) ，则 2π -θ∈[0 ， π ] ，且OBOAcos(2π–θ)=cosθ=cos(α-β) Cα-β差角的余弦公式结论归纳α,β 对于任意角cos()cos cossin sinα-βαβ+αβ注意： 1. 公式的结构特点；2. 对于 α,β, 只要知道其正弦或余弦，就可以求出 cos(α － β) 分析 :cos15cos 4530cos15cos 6045思考：你会求 的值吗 ?sin75例 1. 利用差角余弦公式求 的值cos15学以致用！！cos()cos cossin sinα-βαβ+αβ cos()cos cossin sinα-βαβ+αβ例 2. 已知 2cos, 3α=-α5求 的值 .cos4α解 :2cos, 3α=-α5∵∴24sin1cos5α=αcos()coscossinsin444-αα+α224225 35210练习： P142 .3学以致用！！ cos()cos cossin sinα-βαβ+αβ例 3. 已知 2sin, ，，4α=α5cos，5β=- 13是第三象限角，β学以致用！！求 cos(α-β) 的值 练习：000055sin175sin55cos175cos.121)24sin()21sin()24cos()21cos(.2000022cos()cos cossin sinα-βαβ+αβ 思考题：已知 都是锐角 ,，αβcos，4α=55cos13α+βcos求的值ββ=α+βα变角 :分析：coscossinαβαsincosαβαcos531312541356516三角函数中一定要注意观察角度之间的关系，例如=α+β=(-)+ 两角差的余弦公式小结对于任意角 α,β 都有cos(α-β)=cosαcosβ+sinαsinβ注意： 1. 公式的结构特点；2. 对于 α,β, 只要知道其正弦或余弦，就可以求出 cos(α － β). 再 见