高中数学132函数极值与导数 课件(新人教A版选修2-2) 课件VIP免费

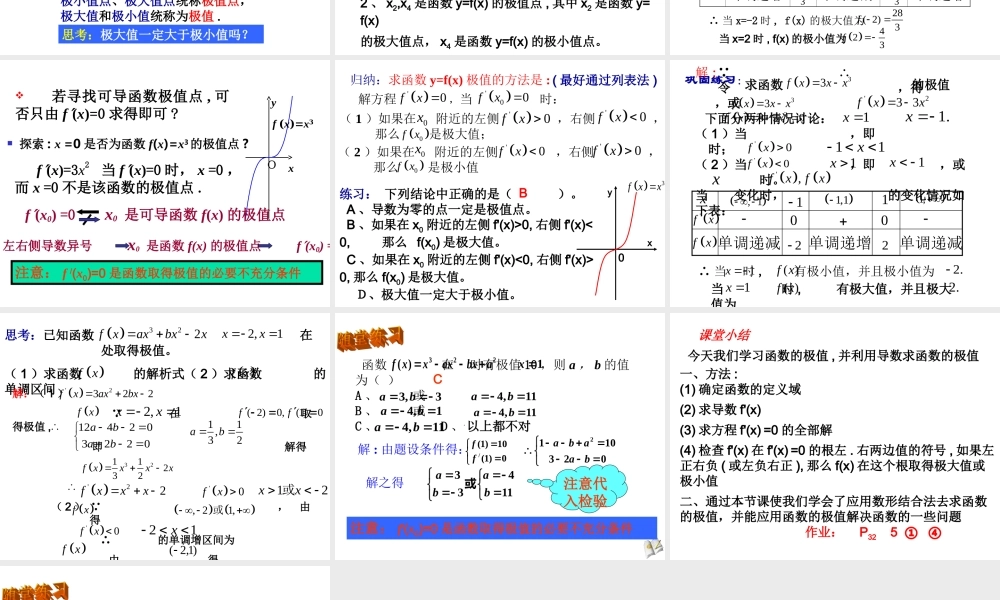
1.3.2 函数极值与导数 知识回顾如果在某个区间内恒有 , 则 为常数 .0)( xf)(xf用“导数法” 求单调区间的步骤 :注意：函数定义域① 求 '( )fx② 令 '( )0( )'( )0( )fxf xfxf x解不等式的递增区间解不等式的递减区间③ 求单调区间aoht '0h a ht问题：如图表示高台跳水运动员的高度 随时间 变化的函数 的图象 2( )4.96.510h ttt单调递增单调递减0)( th0 )(thaat at 归纳 : 函数 在点 处 ,在 的附近 , 当 时 , 函数 h(t) 单调递增， ; 当 时 , 函数 h(t) 单调递减 , 。( )h tta0)( ah0)( th0)( thyxa ob yf x （ 3 ）在点 附近 , 的导数的符号有 什么规律 ?,a b yf x （ 1 ）函数 在点 的函数值与这些点 附近的函数值有什么关系 ? yf x,a b（ 2 ）函数 在点 的导数值是多少 ? yfx,a b( 图一 )问题：0)( xf0)( xf0)( xf0)( af0)( bfxy yf xohgfedc( 图二 )yxa ob yf x( 图一 )0)( xf0)( xf0)( xf0)( af0)( bfxy yf xohgfedc( 图二 )极大值 f(b)点 a 为函数 y=f(x) 的极小值点， f(a) 叫做函数 y=f(x) 的极小值 .点 b 为函数 y=f(x) 的极大值点， f(b) 叫做函数 y=f(x) 的极大值 .极小值点、极大值点统称极值点，极大值和极小值统称为极值 .极小值 f(a)思考：极大值一定大于极小值吗？ yfx6x5x4x3x2x1xabxy （ 1 ）如图是函数的图象 , 试找出函数 的极值点 , 并指出哪些是极大值点 , 哪些是极小值点？o（ 2 ）如果把函数图象改为导函数 的图象 ? 'yfx yf x yf x答： 'yfx1 、 x1,x3,x5,x6 是函数 y=f(x) 的极值点，其中 x1,x5 是函数 y=f(x) 的极大值点， x3,x6 函数 y=f(x) 的极小值点。2 、 x2,x4 是函数 y=f(x) 的极值点 , 其中 x2 是函数 y=f(x)的极大值点， x4 是函数 y=f(x) 的极小值点。 下面分两种情况讨论 : （ 1 ）当，即 x ＞ 2, 或 x ＜ -2 时 ;（ 2 ）当 ，即 -2 ＜ x ＜ 2 时。例 4 ：求函数 的极值 .  31443f xxx 31443f xxx '2422fxxxx '0fx  '0,fx 解 : ∴...