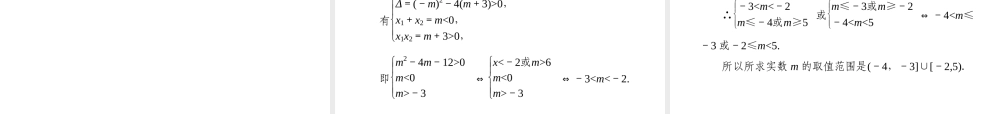• 1 . 2 基本逻辑联结词• 1 .知识与技能• 了解含有“且”“或”的新命题的含义,能判断复合命题的真假.• 2 .过程与方法• 通过学习,体会命题间的逻辑关系.• 3 .情感态度与价值观• 通过学习,让学生体会探索的乐趣,培养学生的创新意识.• 本节重点:理解“且”、“或”的含义,并会判断由其组成的复合命题的真假.• 本节难点:对“或”的含义的理解.• 1 .逻辑联结词“且”与自然语言中的“并且”“和”相当.“或”与自然语言中的“或者”“可能”相当,但自然语言中的“或者”有两种用法:一是“不可兼”的“或”;二是“可兼”的“或”,而我们仅研究可兼“或”在数学中的含义.“非”与日常生活中的“不是”“全盘否定”“问题的反面”相近.而“非”命题,就是对命题的否定.• 2 .通过实例去理解“且”“或”的含义.• 1 .结合例子去总结判断 p∧q , p∨q 形式命题的真假的规律.• 2 .逻辑联结词“且”、“或”与集合的交、并运算有着密切的联系,可以从集合的角度去进一步理解“且”“或”的意义.• 1 .两种基本逻辑联结词.• (1)“ 且”• 逻辑联结词“且”与日常语言中的相当.• (2)“ 或”• 逻辑联结词“或”的意义和日常语言中的“ ”是相当的.• 2 .由“且”与“或”构成的新命题的写法及读法.• (1) 利用逻辑联结词“且”把命题 p 和 q 联结起来,就得到一个新命题,记作,读作“ ”.并且、及、和或者p∧qp 且 q• (2) 用逻辑联结词“或”把命题 p , q 联结起来,就得到一个新命题,记作,读作“ ”.• 3 .含有逻辑联结词“且”与“或”的命题的真假规律 ( 真值表 ) :pqp∧qp∨q真真真真真假假真假真假真假假假假p∨qp 或 q• (2)p:N⊆Z q:{0}⊆N• (3)p:35 是 15 的倍数q:35 是 7 的倍数• (2)p∧qN⊆Z 且 {0}⊆N ,• p∨qN⊆Z 或 {0}⊆N.[例 1] 分别写出由下列各组命题构成的“p∧q”,“p∨q”形式的命题. (1)p: 2是无理数 q: 2大于 1 [解析] (1)p∧q 2是无理数且大于 1, p∨q 2是无理数或大于 1. • (3)p∧q35是 15 的倍数且是 7 的倍数,• p∨q35是 15 的倍数或是 7 的倍数.• [ 说明 ] 解答这类题目的关键是要正确地使用联结词,并注意语法上的要求 .• [ 例 2] 判断下列命题的真假.• (1)2≤2.• (2) 等腰三角形顶角的平分线平分底边并且垂直...