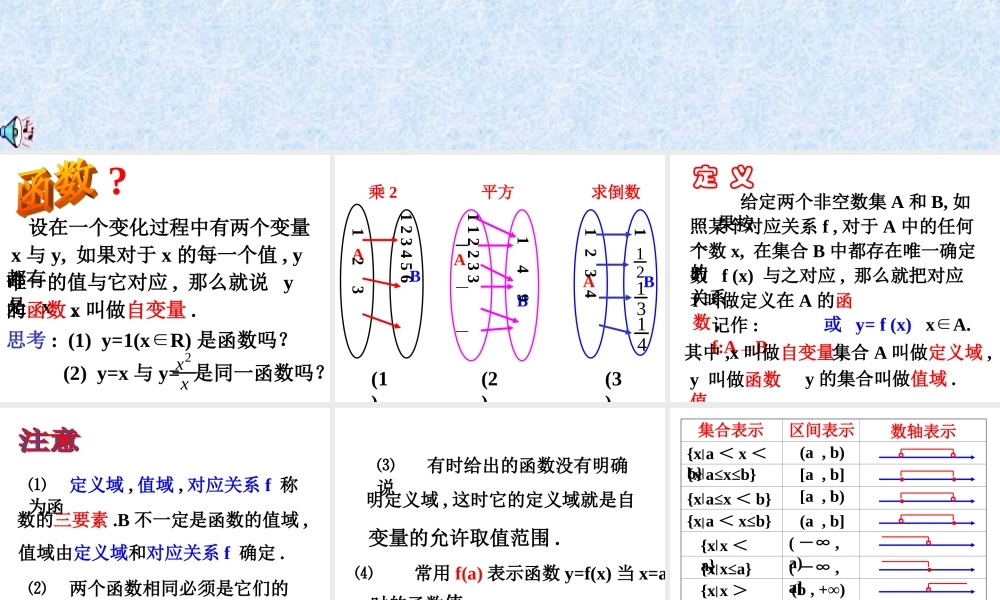
?设在一个变化过程中有两个变量 x 与 y, 如果对于 x 的每一个值 , y都有唯一的值与它对应 , 那么就说 y是 x的函数 . 思考 : (1) y=1(xR)∈是函数吗? (2) y=x 与 y=2xx 是同一函数吗?x 叫做自变量 . AAABBB 1 2 3 1 2 3 4 5 6 1 1 2 2 3 3 1 4 9 --- 1 2 3 4 1 121314(1)(2)(3)乘 2平方求倒数 定 义 给定两个非空数集 A 和 B, 如果按照某个对应关系 f , 对于 A 中的任何一个数 x, 在集合 B 中都存在唯一确定的数 f (x) 与之对应 , 那么就把对应关系f 叫做定义在 A 的函数 .记作 : f:A→B其中 ,x 叫做自变量 , y 叫做函数值 , 集合 A 叫做定义域 ,y 的集合叫做值域 .或 y= f (x) xA.∈ ⑴ 定义域 , 值域 , 对应关系 f 称为函数的三要素 .B 不一定是函数的值域 ,⑵ 两个函数相同必须是它们的定义域和对应关系分别完全相同 .值域由定义域和对应关系 f 确定 . ⑶ 有时给出的函数没有明确说⑷ 常用 f(a) 表示函数 y=f(x) 当 x=a明定义域 , 这时它的定义域就是自变量的允许取值范围 .时的函数值 . 集合表示区间表示数轴表示{x a < x <b}(a , b)。。{x a≤x≤b}[a , b]..{x a≤x < b}[a , b).。{x a < x≤b}(a , b].。{x x <a}( -∞ , a)。{x x≤a}( -∞ , a].{x x >b}(b , +∞)。{x x≥b}[b , +∞).{x xR}∈( -∞ ,+∞) 数轴上所有的点 1. 一次函数 y=ax+b(a≠0) 定义域是R.值域是R. 二次函数 y=ax2+bx+c (a≠0) 的定义域是 R.值域是当 a > 0 时 ,为 :244{}ac bay y当 a < 0 时 , 为 :244{}ac bay y 2. 某山海拔 7500m, 海平面温度为 250C, 气温是高度的函数 , 而且高度每升高 100m, 气温下降0.60C. 请你用解析表达式表示出气温 T 随高度 x 变化的函数 , 并指出其定义域和值域 . 3. 已知 f (x)=3x2 - 5x+2,求f(3),f( - ),f(a),f(a+1),f[f(a)].2 4. 下列函数中与函数 y=x 相同的是 ( ).A. y=( )2 ; B. y= ;x33xC. y= .2xB 课堂练习1. 已知 f (x)=3x -2, 求 f (0), f (3) 和函数的值域 .2. 教材 P35T1,2.x{0,1,2,3,5}∈ 作 业2. 若 f(x)=ax2 - , 且2( 2)2,ff 求 a.1. 若 f(0)=1 , f(n)=nf(n -1), nN求f(4).3. 已知 g(x)=1 -2x, 22112( )(0),( ).xxf g xxf求