高中数学函数的概念课件 苏教版 必修1 课件VIP免费

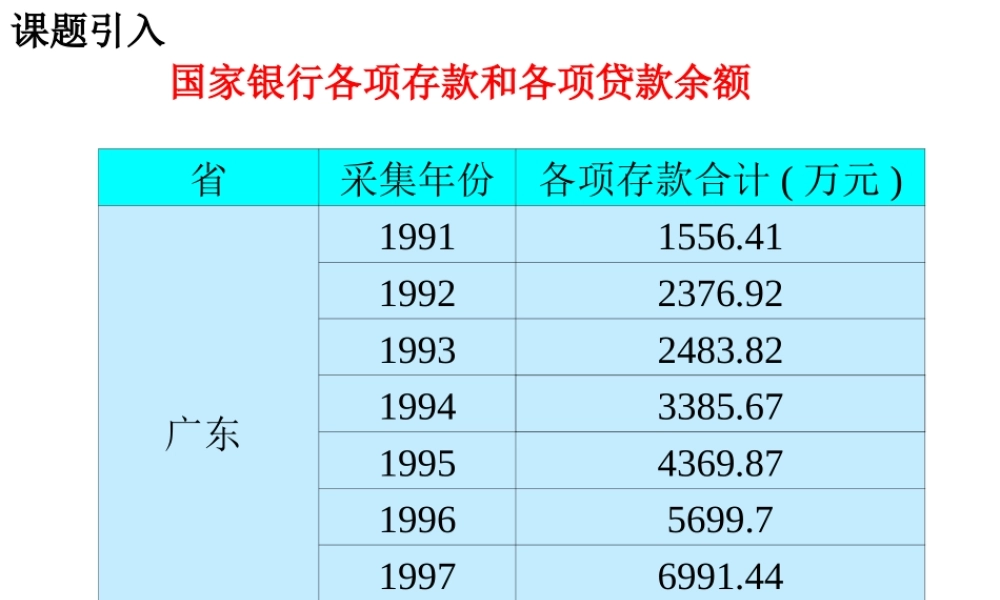
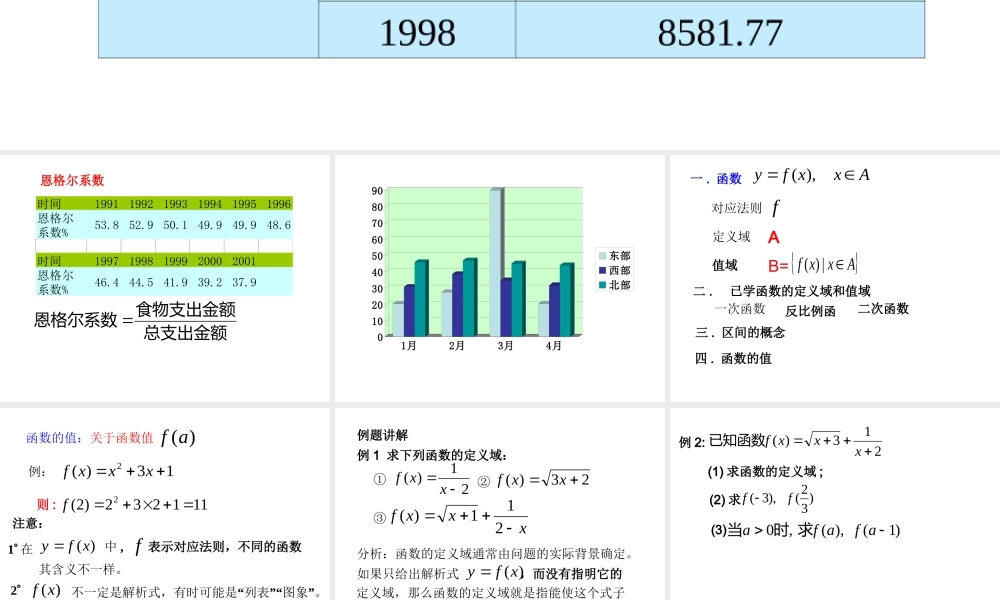
省采集年份各项存款合计 ( 万元 )广东 19911556.4119922376.9219932483.8219943385.6719954369.8719965699.719976991.4419988581.77国家银行各项存款和各项贷款余额 课题引入 时间199119921993199419951996恩格尔系数%53.852.950.149.949.948.6时间19971998199920002001恩格尔系数%46.444.541.939.237.9恩格尔系数总支出金额食物支出金额恩格尔系数  01020304050607080901月2月3月4月东部西部北部 一 . 函数Axxfy),(fAxxf|)(对应法则定义域值域B=A二 . 已学函数的定义域和值域一次函数反比例函 二次函数 三 . 区间的概念四 . 函数的值 函数的值：关于函数值 )(af13)(2xxxf例：111232)2(2f则 :)(xfy f1 在中 , 其含义不一样。表示对应法则，不同的函数2)(xf“”“”不一定是解析式，有时可能是 列表图象 。注意：)(xf)(af 3与是不同的，前者为变数，后者为常数。 例题讲解例 1 求下列函数的定义域：21)(xxf23)(xxfxxxf211)( ① ② ③)(xfy x分析：函数的定义域通常由问题的实际背景确定。 如果只给出解析式，而没有指明它的定义域，那么函数的定义域就是指能使这个式子有意义的实数的集合。 213)(xxxf已知函数例 2: (1) 求函数的定义域 ;)32(),3(ff (2) 求(3))1(),(,0afafa求时当 例 3 下列函数中哪个与函数xy  是同一个函数？2xy 33xy 2xy ⑴⑵⑶xx2)4( 下列各组中的两个函数是否为相同的函数？ 3)5)(3(1xxxy52xy① （定义域不同）111xxy)1)(1(2xxy② （定义域不同）21)52()(xxf52)(2 xxf③ （定义域、值域都不同） 一 . 函数Axxfy),(fAxxf|)(对应法则定义域值域B=A二 . 已学函数的定义域和值域一次函数反比例函 二次函数 三 . 区间的概念四 . 函数的值小结 :