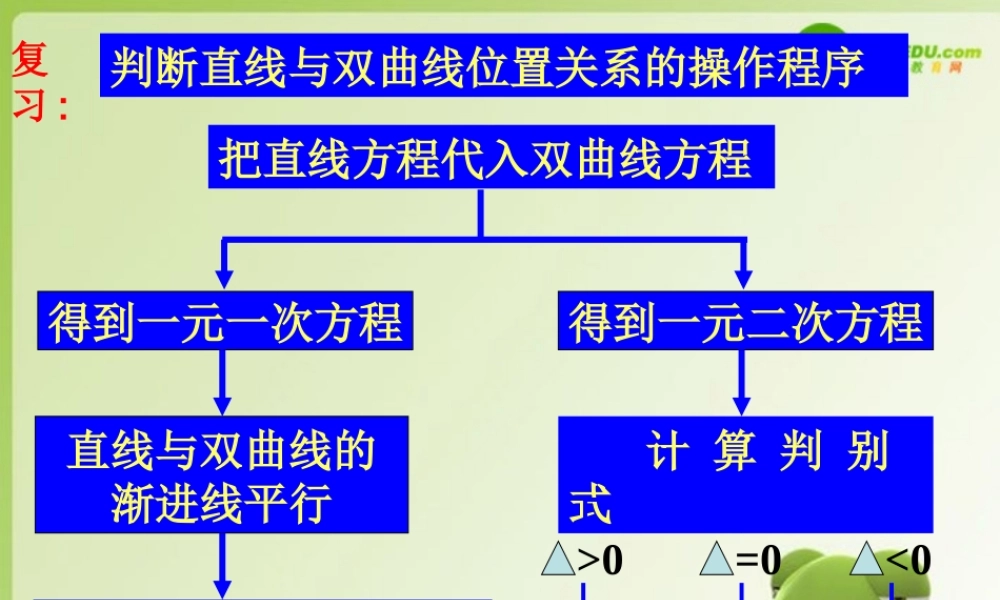
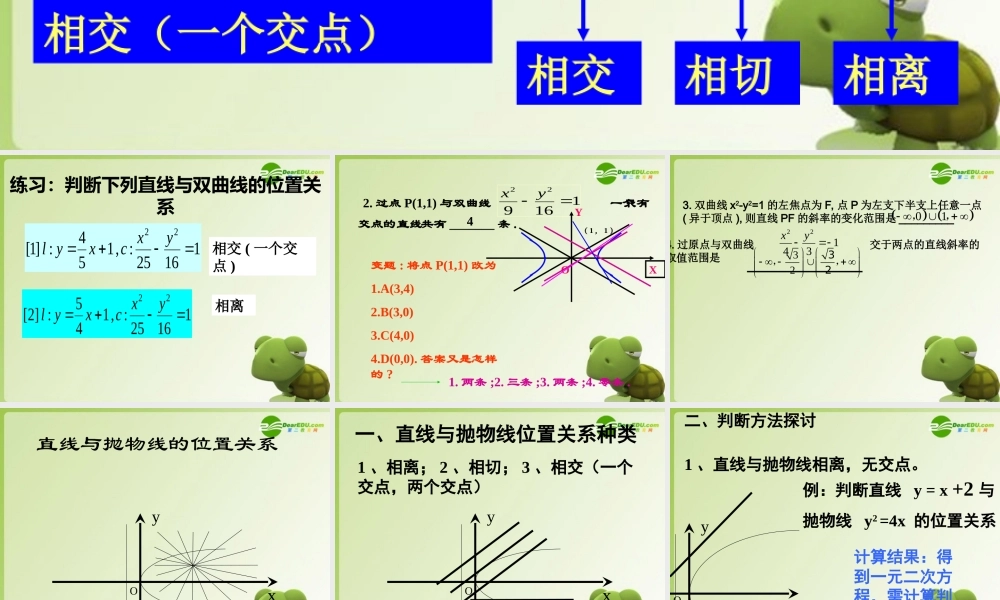
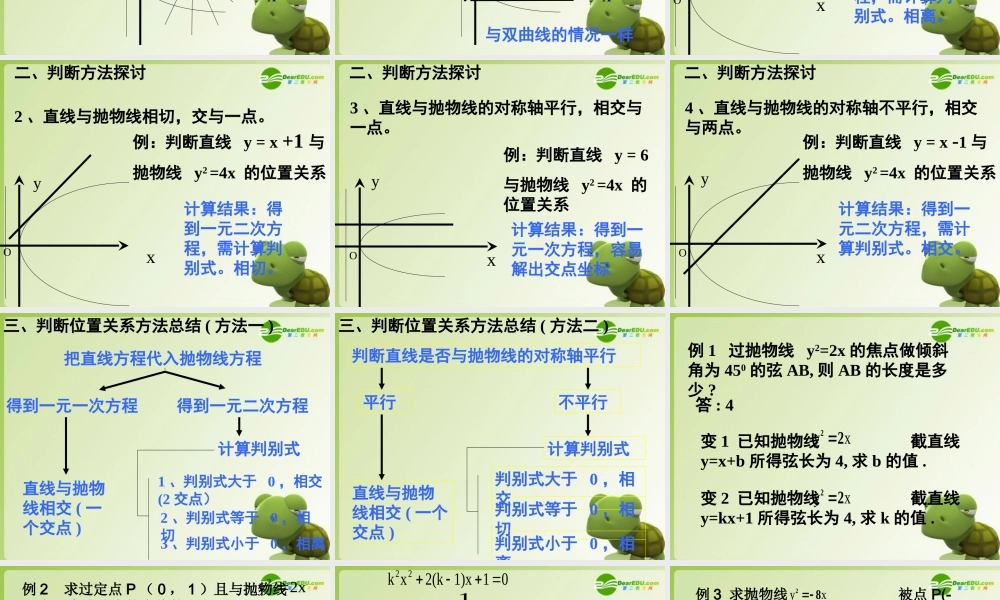
判断直线与双曲线位置关系的操作程序把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐进线平行相交(一个交点) 计 算 判 别 式>0=0<0相交相切相离复习 : 练习:判断下列直线与双曲线的位置关系相交 ( 一个交点 )11625:,145:]2[22yxcxyl相离11625:,154:]1[22yxcxyl 2. 过点 P(1,1) 与双曲线 只有共有 _______ 条 . 变题 : 将点 P(1,1) 改为1.A(3,4) 2.B(3,0)3.C(4,0)4.D(0,0). 答案又是怎样的 ?4116922 yx1. 两条 ;2. 三条 ;3. 两条 ;4. 零条 .交点的一个直线XYO( 1 , 1 )。 3. 双曲线 x2-y2=1 的左焦点为 F, 点 P 为左支下半支上任意一点( 异于顶点 ), 则直线 PF 的斜率的变化范围是 _________ 01 ,,4. 过原点与双曲线 交于两点的直线斜率的取值范围是 13422 yx32 3,,2 xyO直线与抛物线的位置关系 一、直线与抛物线位置关系种类xyO1 、相离; 2 、相切; 3 、相交(一个交点,两个交点)与双曲线的情况一样 xyO二、判断方法探讨1 、直线与抛物线相离,无交点。例:判断直线 y = x +2 与抛物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相离。 xyO二、判断方法探讨2 、直线与抛物线相切,交与一点。例:判断直线 y = x +1 与抛物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相切。 xyO二、判断方法探讨3 、直线与抛物线的对称轴平行,相交与一点。例:判断直线 y = 6与抛物线 y2 =4x 的位置关系计算结果:得到一元一次方程,容易解出交点坐标 xyO二、判断方法探讨例:判断直线 y = x -1 与抛物线 y2 =4x 的位置关系计算结果:得到一元二次方程,需计算判别式。相交。4 、直线与抛物线的对称轴不平行,相交与两点。 三、判断位置关系方法总结 ( 方法一 )把直线方程代入抛物线方程得到一元一次方程得到一元二次方程直线与抛物线相交 ( 一个交点 )计算判别式1 、判别式大于 0 ,相交(2 交点)2 、判别式等于 0 ,相切3 、判别式小于 0 ,相离 三、判断位置关系方法总结 ( 方法二 )判断直线是否与抛物线的对称轴平行不平行直线与抛物线相交 ( 一个交点 )计算判别式判别式大于 0 ,相交判别式等于 0 ,相切判别式小于 0 ,相离平行 ...