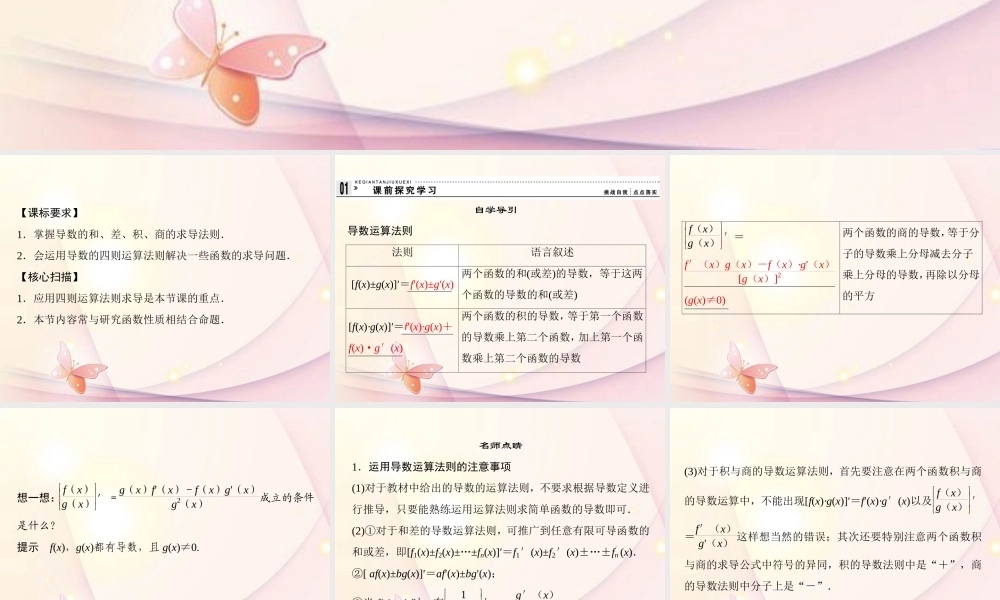
第 2 课时 导数的运算法则【课标要求】 1.掌握导数的和、差、积、商的求导法则. 2.会运用导数的四则运算法则解决一些函数的求导问题. 【核心扫描】 1.应用四则运算法则求导是本节课的重点. 2.本节内容常与研究函数性质相结合命题. 自学导引 导数运算法则 法则 语言叙述 [f(x)±g(x)]′=f′(x)±g′(x) 两个函数的和(或差)的导数,等于这两个函数的导数的和(或差) [f(x)·g(x)]′=f′(x)·g(x)+f(x)·g′(x) 两个函数的积的导数,等于第一个函数的导数乘上第二个函数,加上第一个函数乘上第二个函数的导数 f(x)g(x) ′=f′(x)g(x)-f(x)·g′(x)[g(x)]2(g(x)≠0) 两个函数的商的导数,等于分子的导数乘上分母减去分子乘上分母的导数,再除以分母的平方 想一想:f(x)g(x) ′=g(x)f′(x)-f(x)g′(x)g2(x)成立的条件是什么? 提示 f(x),g(x)都有导数,且 g(x)≠0. 名师点睛 1.运用导数运算法则的注意事项 (1)对于教材中给出的导数的运算法则,不要求根据导数定义进行推导,只要能熟练运用运算法则求简单函数的导数即可. (2)①对于和差的导数运算法则,可推广到任意有限可导函数的和或差,即[f1(x)±f2(x)±…±fn(x)]′=f1′(x)±f2′(x)±…±f′n (x). ②[ af(x)±bg(x)]′=af′(x)±bg′(x); ③当 f(x)=1 时,有1g(x) ′=-g′(x)g2(x) . (3)对于积与商的导数运算法则,首先要注意在两个函数积与商的导数运算中,不能出现[f(x)·g(x)]′=f′(x)·g′(x)以及f(x)g(x) ′=f′(x)g′(x) 这样想当然的错误;其次还要特别注意两个函数积与商的求导公式中符号的异同,积的导数法则中是“+”,商的导数法则中分子上是“-”. 2.变形化简,减少求导的运算量 应用和、差、积的求导法则和常见函数的导数公式求导数时,在可能的情况下,应尽量少用甚至不用乘积和商的求导法则,应在求导之前,先利用代数、三角恒等变形对函数进行化简,然后再求导,这样可以减少运算量,提高运算速度,避免出错. 题型一 求导法则的直接运用 【例 1】 求下列函数的导数. (1)y=3x-lg x; (2)y=(x2+1)(x+1); (3)y= x+3x2+3; (4)y=-sin x+ex. [思路探索] 解答本题可根据函数导数的四则运算法则和导数公式求导. 解 (1)y′=(3x)′-(lg x)′=3x·ln 3-1xln...