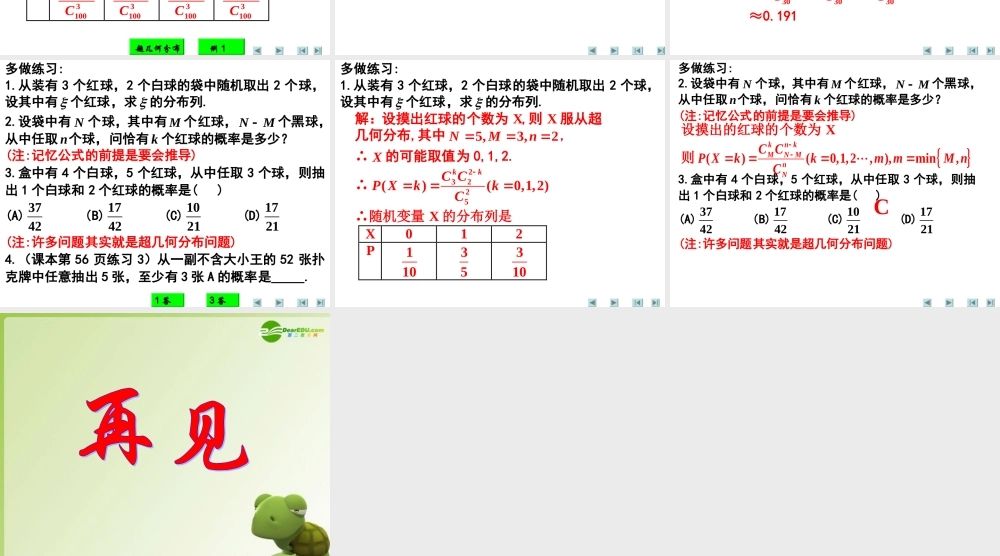
2.1.3 《离散型随机变量及其分布列 - 超几何分布》 教学目标 • 1 、理解理解超几何分布;• 2 、了解超几何分布的应用. • 教学重点:• 1 、理解理解超几何分布;• 2 、了解超几何分布的应用 超几何分布多做练习开门见山介绍两点分布离散型随机变量的分布列(三) 今天,这节课我们来认识两个特殊的分布列. 首先,看一个简单的分布列─两点分布列: 如果随机变量的分布列为: 这样的分布列称为两点分布列,称随机变量服从两点分布,而称(1)pP 为成功概率. 两点分布列的运用非常广泛.试举一个例子. 离散型随机变量的分布列(三) 什么是超几何分布? 先思考一个例子: 思考 1.在含有 5 件次品的 100 件产品中,任取 3件,求取到的次品数 X 的分布列. 超几何分布例 1解: X 的可能取值为 0,1,2,3. 又 35953100()(0,1,2,3)kkC CP XkkC ∴随机变量 X 的分布列是 X 0 1 2 3 P 035953100C CC 125953100C CC 215953100C CC 305953100C CC 超几何分布: 一般地, 在含有 M 件次品的 N 件产品中,任取 n件,其中恰有 X 件次品数,则事件Xk发生的概率为()(0,1,2,,)kn kMNMnNC CP XkkmC其中min,mM n,且*,, ,,nN MN n M NN≤≤. 称随机变量 X 的分布列为超几何分布列,且称随机变量 X 服从超几何分布 注:⑴超几何分布的模型是不放回抽样 ⑵超几何分布中的参数是 M,N,n 例 1.在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有 10 个红球和 20 个白球,这些球除颜色外完全相同.游戏者一次从中摸出 5 个球.至少摸到 3个红球就中奖,求中奖的概率. 解:设摸出红球的个数为 X,则 X 服从超几何分布,其中30,10,5NMn ,于是由超几何分布模型得中奖的概率 (3)(3)(4)(5)P XP XP XP X≥ 324150102010201020555303030C CC CC CCCC ≈0.191 多做练习: 1.从装有 3 个红球,2 个白球的袋中随机取出 2 个球,设其中有 个红球,求 的分布列. 2.设袋中有 N 个球,其中有 M 个红球,NM个黑球,从中任取 n个球,问恰有 k 个红球的概率是多少? (注:记忆公式的前提是要会推导) 3.盒中有 4 个白球,5 个红球,从中任取 3 个球,则抽出 1 个白球和 2 个红球的概率是( ) (A) 3742 (B) 1742 (C) 1021 (D) 1721 (注:许多问题其实就是超几何分布问题) 4.(...