高中数学 双曲线弦长问题课件 新人教A版选修2-1 课件VIP免费

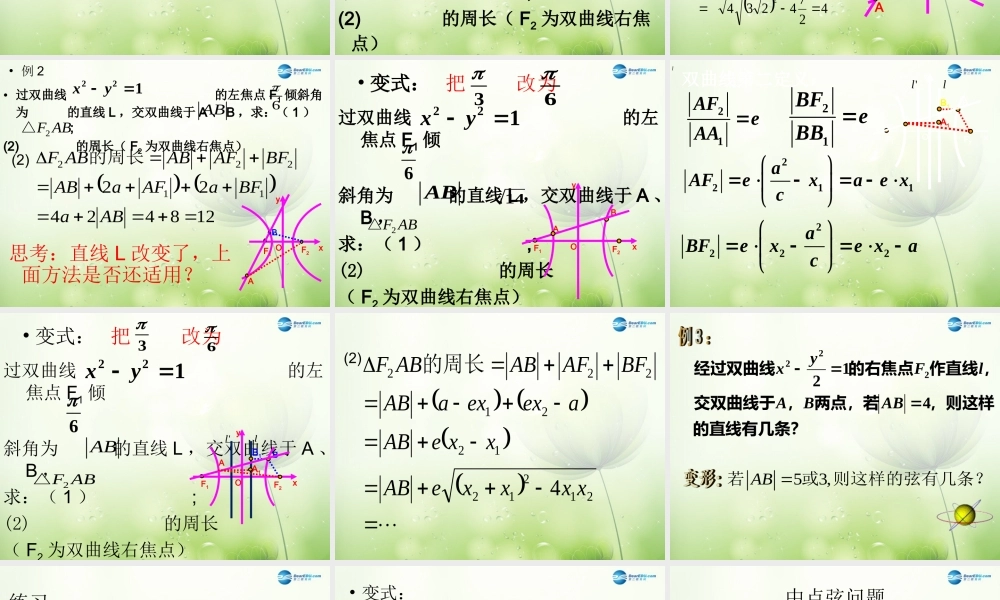
双曲线的弦长问题 直线与双曲线的位置关系与交点个数0 个交点：相离1 个交点：特殊的相交 ( 与渐近线平行 ) 或相切2 个交点：相交XYO判断直线与双曲线位置关系的方法把直线方程代入双曲线方程得到一元一次方程得到一元二次方程直线与双曲线的渐近线平行相交（一个交点） 计 算 判 别 式>0=0<0相交相切相离|AB| 22121214kxxx x（）212122114yyy yk  2（）弦长公式或|AB| • 例 122123yx  求直线 被双曲线 截得的弦长。10xy 4 6• 例 2221xy过双曲线 的左焦点 F1 倾斜角为 的直线 L ，交双曲线于 A 、B ，求：（ 1 ） ;(2) 的周长（ F2 为双曲线右焦点）3ABABF2△• 例 2221xy• 过双曲线 的左焦点 F1 倾斜角为 的直线 L ，交双曲线于 A 、 B ，求：（ 1 ） ;(2) 的周长（ F2 为双曲线右焦点）3ABABF2△23xyl的方程为：07262123222xxyxxy由 4274234221221241xxxxkAB解 :(1)OxyF1F2BA• 例 2221xy• 过双曲线 的左焦点 F1 倾斜角为 的直线 L ，交双曲线于 A 、 B ，求：（ 1 ） ;(2) 的周长（ F2 为双曲线右焦点）6ABABF2△(2) 1284242211222ABaBFaAFaABBFAFABABF的周长xOyF1F2BA思考：直线 L 改变了，上面方法是否还适用？• 变式：221xy过双曲线 的左焦点 F1 倾斜角为 的直线 L ，交双曲线于 A 、B ，求：（ 1 ） ;(2) 的周长（ F2 为双曲线右焦点）6AB把 改为36OxyF1F2BA14ABF2△l双曲线第二定义： 21AFeAA21BFeBB2211aAFexae xc  2222aBFexe xac  B1OxyF1F2Bl'lAA1• 变式：221xy过双曲线 的左焦点 F1 倾斜角为 的直线 L ，交双曲线于 A 、B ，求：（ 1 ） ;(2) 的周长（ F2 为双曲线右焦点）6ABABF2△把 改为36B1OxyF1F2Bl'lAA1(2) 2121212212224 xxxxeABxxeABaexexaABBFAFABABF的周长的直线有几条？，则这样两点，若，交双曲线于，作直线的右焦点经过双曲线412222ABBAlFyx53,AB 若或 则这样的弦有几条？• 已知倾斜角为 的直线 L 被双曲线 截得的弦长 ，求直线 L 的...