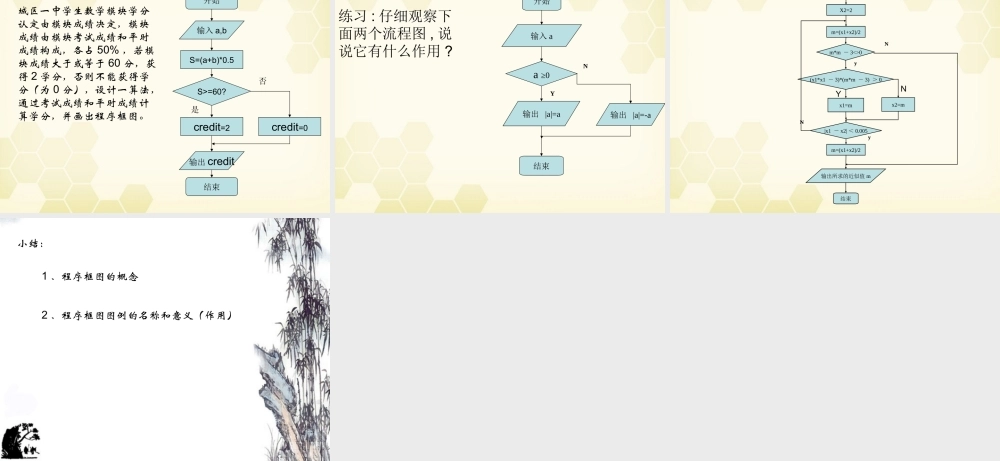
§1.1.2 程序框图 复习1 、算法的概念2 、算法的特点3 、常见的几个例子4 、判断一个正整数是否是质数的算法 算法的概念算法是指解决给定问题的有穷操作步骤的描述,简单的说,算法就是解决问题的步骤和方法。 算法的基本特点1 、有穷性一个算法应包括有限的操作步骤,能在执行有穷的操作步骤之后结束。2 、确定性算法的计算规则及相应的计算步骤必须是唯一确定的,既不能含糊其词,也不能有二义性。3 、有序性算法中的每一个步骤都是有顺序的 , 前一步是后一步的前提 , 只有执行完前一步后 , 才能执行后一步 , 有着很强逻辑性的步骤序列。 判断一个正整数是否是质数的算法自然语言描述图形描述第一步:判断 n 是否等于 2 ?若 n=2 ,则n 是质数,否则,执行第二步;第二步:依次从 2~( n-1 )检验是不是 n 的因数,即能整除 n 的数,若有这样的数,则 n 不是质数;若没有,则 n 是质数。开始输入 n求 n 除以 i 的余数i 的值增加 1, 仍用 i 表示i>n-1 或 r=0?r=0?n 不是质数n 是质数结束否否是是i=2 判断一个正整数是否是质数的算法图形描述思考:1 、 r 的作用是什么?2 、 i 的值增加 1(i=i+1) 有什么作用?3 、整个图形中有哪些基本的图形,各自的意义和作用是什么?开始输入 n求 n 除以 i 的余数i 的值增加 1, 仍用 i 表示i>n-1 或 r=0?r=0?n 不是质数n 是质数结束否否是是i=2 程序框图又称流程图,是一种用规定的图形,指向线及文字说明来准确、直观地表示算法的图形。程序框名称功能终端框(起止框)表示一个算法的起始和结束输入、输出框表示算法的输入和输出的信息处理框(执行框)赋值、计算判断框判断一个条件是否成立,用“是”、“否”或“ Y” 、“ N” 标明 例 1 设计一算法:输入圆的半径 , 输出圆的面积,并画出流程图算法分析:第一步:输入圆的半径第二步:利用公式“圆的面积 = 圆周率 × (半径的平方)”计算圆的面积;第三步:输出圆的面积。开始结束输入半径 R计算 S=Pi*R*R输出面积 S定义 Pi=3.14思考:整个程序框图有什么特点? 例 2 已知一个三角形的三边长分别为 2,3,4, 利用海伦 - 秦九韶公式设计一个算法 , 求出它的p= ( 2+3+4 ) /2s=SQR(p*(p - 2)*(p - 3)*(p-4))输出 s结束开始面积 , 画出算法的程序框图 . 例 3 设计房租收费的算法 , 其要求是 : 住房面积 80 平方米以内 , ...