高中数学 13(空间几何体的表面积与体积)(第2课时)课件 新人教版A必修2 课件VIP免费

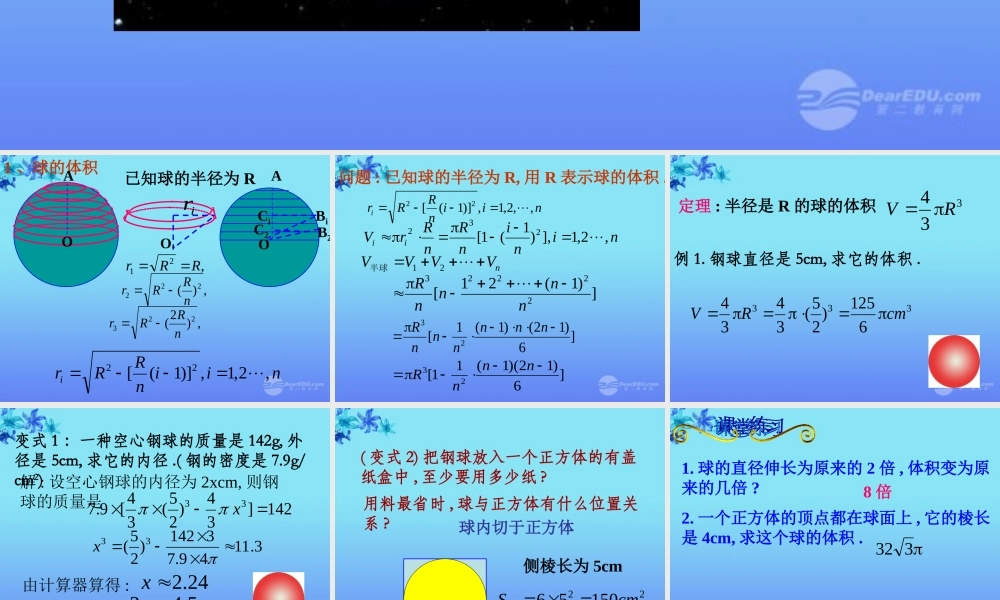
1.3.2 球的体积和表面积AOirO.niinRRri,2,1,)]1([22,21RRr,)(222nRRr1 、球的体积B2C2BiCiAO,)2(223nRRr已知球的半径为 RnininRnRrVii,2,1],)1(1[232问题 : 已知球的半径为 R, 用 R 表示球的体积 .niinRRri,,2,1,)]1([22nVVVV21半球])1(21[22223nnnnR]6)12()1(1[23nnnnnnR]6)12)(1(11[23nnnR例 1. 钢球直径是 5cm, 求它的体积 .3336125)25(3434cmRV334 RV定理 : 半径是 R 的球的体积变式 1 ：一种空心钢球的质量是 142g, 外径是 5cm, 求它的内径 .( 钢的密度是 7.9g/cm2)解 : 设空心钢球的内径为 2xcm, 则钢球的质量是答 : 空心钢球的内径约为 4.5cm.142] 34)25(34[9.733x3.1149.73142)25(33x由计算器算得 :24.2x5.42 x( 变式 2) 把钢球放入一个正方体的有盖纸盒中 , 至少要用多少纸 ?用料最省时 , 球与正方体有什么位置关系 ?球内切于正方体2215056cmS侧侧棱长为 5cm1. 球的直径伸长为原来的 2 倍 , 体积变为原来的几倍 ?2. 一个正方体的顶点都在球面上 , 它的棱长是 4cm, 求这个球的体积 . 8 倍332变式 3. 有三个球 , 一球切于正方体的各面 ,一球切于正方体的各侧棱 , 一球过正方体的各顶点 , 求这三个球的体积之比 .作轴截面例 2 、某街心花园有许多钢球（钢的密度是 7.9g/cm3), 每个钢球重 145kg ，并且外径等于 50cm ，试根据以上数据，判断钢球是实心的还是空心的。如果是空的 , 请你计算出它的内径（ π 取 3.14 ，结果精确到 1cm ）。1. 两种方法 : 化整为零的思想方法和“分割 ,求和 , 取极限”的数学方法 .2. 一个观点 : 在一定条件下 , 化曲为直的辨证观点 .3. 一个公式 : 半径为 R 的球的体积是334 RV4. 解决两类问题 : 两个几何体相切和相接作适当的轴截面两个几何体相切 : 一个几何体的各个面与另一个几何体的各面相切 .两个几何体相接 : 一个几何体的所有顶点都 在另一个几何体的表面上球面：半圆以它的直径为旋转轴，旋转所成的曲面。球 ( 即球体 ): 球面所围成的几何体。它包括球面和球面所包围的空间。半径是 R 的球的体积：推导方法：334 RV 分割求近似和化为准确和小结：第一步：分割O球面被分割成 n 个网格， ...