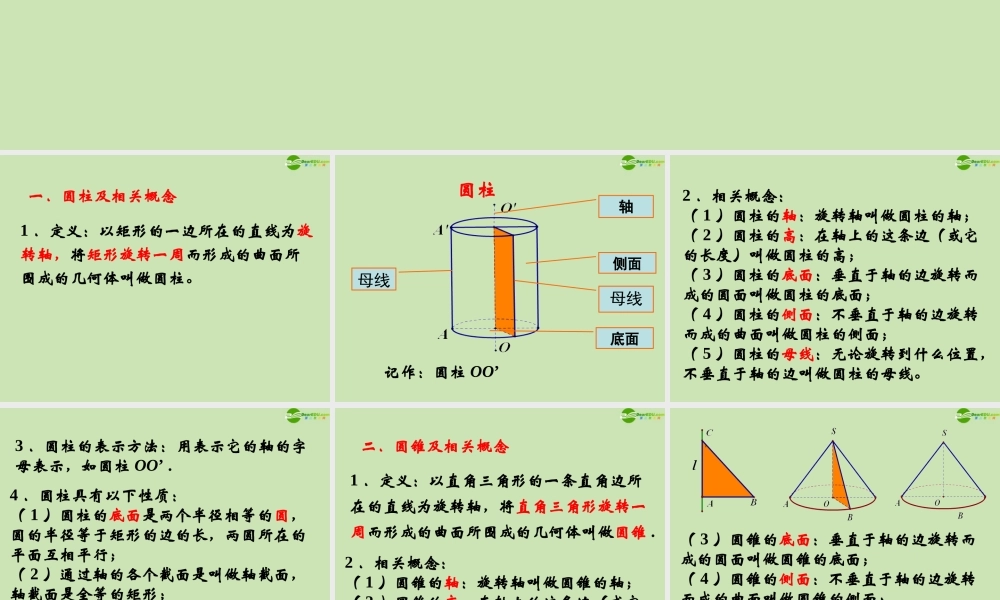
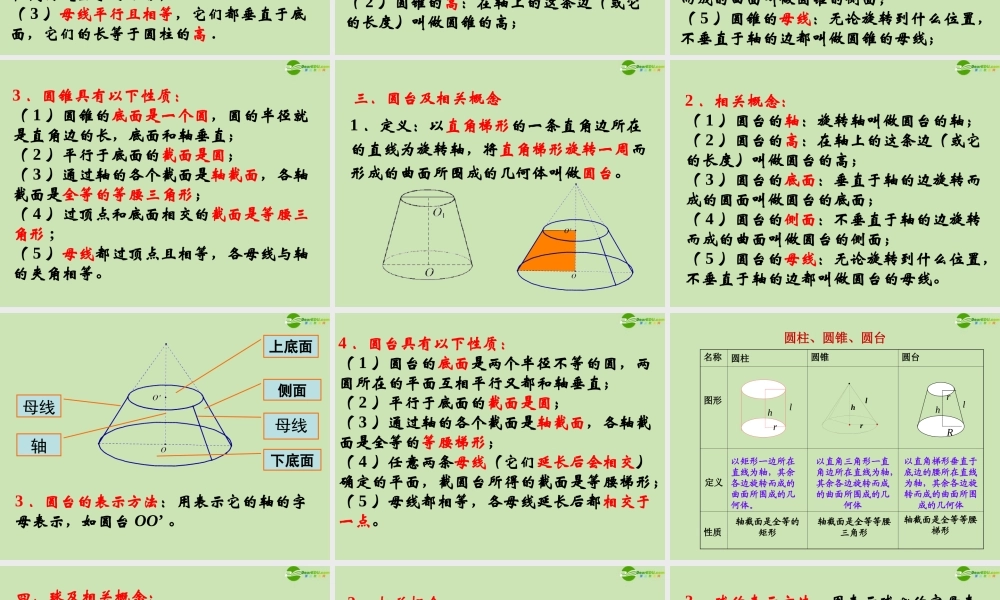
1.1.3 圆柱、圆锥、圆台和球 一.圆柱及相关概念 1 .定义:以矩形的一边所在的直线为旋转轴,将矩形旋转一周而形成的曲面所围成的几何体叫做圆柱。 圆柱侧面轴母线底面记作:圆柱 OO’母线 2 .相关概念:( 1 )圆柱的轴:旋转轴叫做圆柱的轴;( 2 )圆柱的高:在轴上的这条边(或它的长度)叫做圆柱的高;( 3 )圆柱的底面:垂直于轴的边旋转而成的圆面叫做圆柱的底面;( 4 )圆柱的侧面:不垂直于轴的边旋转而成的曲面叫做圆柱的侧面;( 5 )圆柱的母线:无论旋转到什么位置,不垂直于轴的边叫做圆柱的母线。 3 .圆柱的表示方法:用表示它的轴的字母表示,如圆柱 OO’ .4 .圆柱具有以下性质:( 1 )圆柱的底面是两个半径相等的圆,圆的半径等于矩形的边的长,两圆所在的平面互相平行;( 2 )通过轴的各个截面是叫做轴截面,轴截面是全等的矩形;( 3 )母线平行且相等,它们都垂直于底面,它们的长等于圆柱的高 . 二.圆锥及相关概念 1 .定义:以直角三角形的一条直角边所在的直线为旋转轴,将直角三角形旋转一周而形成的曲面所围成的几何体叫做圆锥 .2 .相关概念:( 1 )圆锥的轴:旋转轴叫做圆锥的轴;( 2 )圆锥的高:在轴上的这条边(或它的长度)叫做圆锥的高; ( 3 )圆锥的底面:垂直于轴的边旋转而成的圆面叫做圆锥的底面;( 4 )圆锥的侧面:不垂直于轴的边旋转而成的曲面叫做圆锥的侧面;( 5 )圆锥的母线:无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线; 3 .圆锥具有以下性质:( 1 )圆锥的底面是一个圆,圆的半径就是直角边的长,底面和轴垂直;( 2 )平行于底面的截面是圆;( 3 )通过轴的各个截面是轴截面,各轴截面是全等的等腰三角形;( 4 )过顶点和底面相交的截面是等腰三角形 ;( 5 )母线都过顶点且相等,各母线与轴的夹角相等。 三.圆台及相关概念 1 .定义:以直角梯形的一条直角边所在的直线为旋转轴,将直角梯形旋转一周而形成的曲面所围成的几何体叫做圆台。 2 .相关概念:( 1 )圆台的轴:旋转轴叫做圆台的轴;( 2 )圆台的高:在轴上的这条边(或它的长度)叫做圆台的高;( 3 )圆台的底面:垂直于轴的边旋转而成的圆面叫做圆台的底面;( 4 )圆台的侧面:不垂直于轴的边旋转而成的曲面叫做圆台的侧面;( 5 )圆台的母线:无论旋转到什么位置,不垂直于轴的边都叫做圆台的母线。 侧面上底面母线下...