高中数学 第二章对数函数(2)课件 苏教版必修1 课件VIP免费

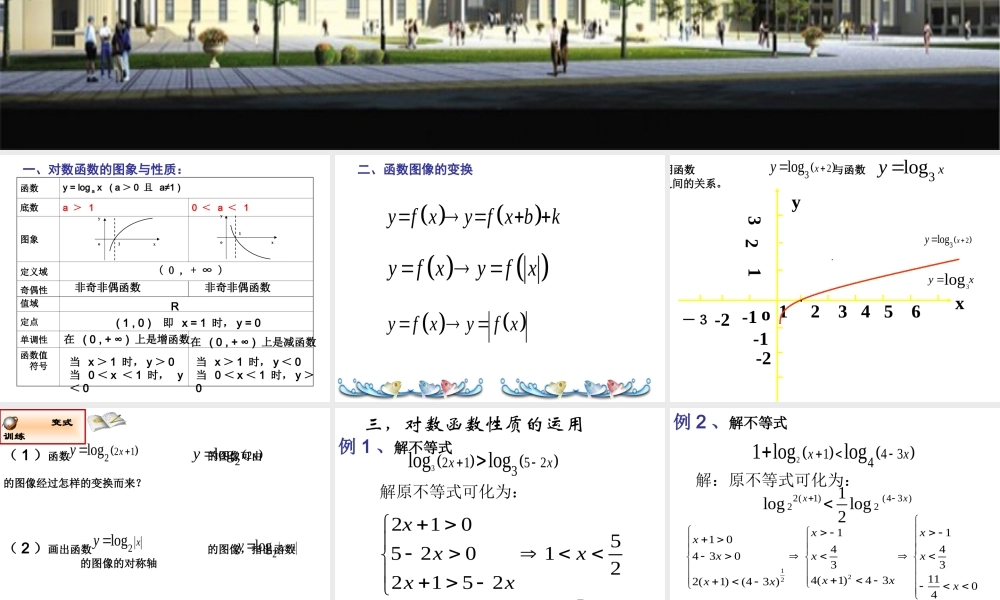
一、对数函数的图象与性质：函数y = log a x ( a ＞ 0 且 a≠1 )底数a ＞ 10 ＜ a ＜ 1图象定义域奇偶性值域定点单调性函数值 符号1xyo1xyo非奇非偶函数非奇非偶函数( 0 , + ∞ )R( 1 , 0 ) 即 x = 1 时， y = 0在 ( 0 , + ∞ ) 上是增函数在 ( 0 , + ∞ ) 上是减函数当 x ＞ 1 时， y ＞ 0当 0 ＜ x ＜ 1 时， y＜ 0当 x ＞ 1 时， y ＜ 0当 0 ＜ x ＜ 1 时， y ＞0 二、函数图像的变换 y f xy f x bk   yf xyfx  yf xyf x 例、说明函数 与函数 的图像之间的关系。23logxy3log xy 3logyx－３xyo 1 2 3 4 5 6 123-1-2-2 -1·23logxy· 变式训练（ 1 ）函数 的图像可由 的图像经过怎样的变换而来？ 212logxy22logxy （ 2 ）画出函数 的图像，指出函数 的图像的对称轴2logxy 12logxy 例 1 、解不等式3 215 23loglogxx解原不等式可化为：2105520122152xxxxx   故原不等式的解集为5{ |1}2xx三，对数函数性质的运用 例 2 、解不等式214 34 1 loglogxx12211104443033114(1)432(1)(43 )0410xxxxxxxxxxxx    2(1)(4 3 )221loglog2xx解：原不等式可化为：故原不等式的解集为 { | 10}xx 例 3 ．求下列函数的定义域12(1)411log xyx23)2(log12xyx引申：已知 的定义域为 ， 求函数 )(xfy 的定义域)]3([log21xfy]1,1[11 1(0, )( , ]44 22(,1)(1,)37[,5]2 例 4 、判断下列函数的奇偶性21) f(x) ln 1xex22 f(x) lg1xx）12222( )()lg(1)lg(1)lg(1)( )( )f xRfxxxxxxxf xf x）析：定义域为 ，为奇函数xxfRxfeexx)1ln()()(22，定义域为解：为偶函数)()()1ln(ln)1ln(222xfxfxxeeexxx 1 log,1axf xx已知13,2f  且12f 则变式：－ 3 例 5 、求下列函数的值域  22 log412fxx   1 log13f xx221122244l...