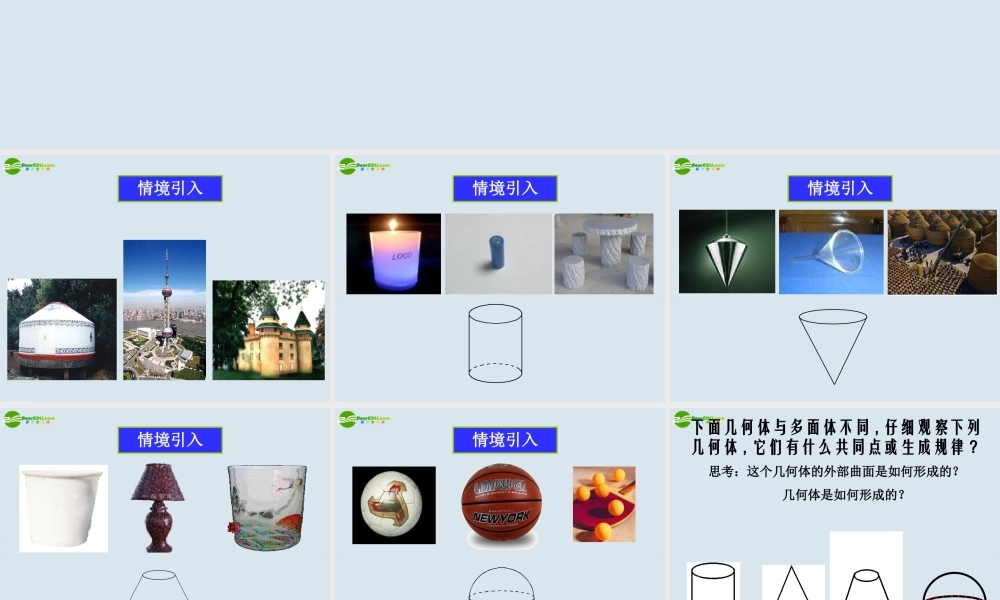
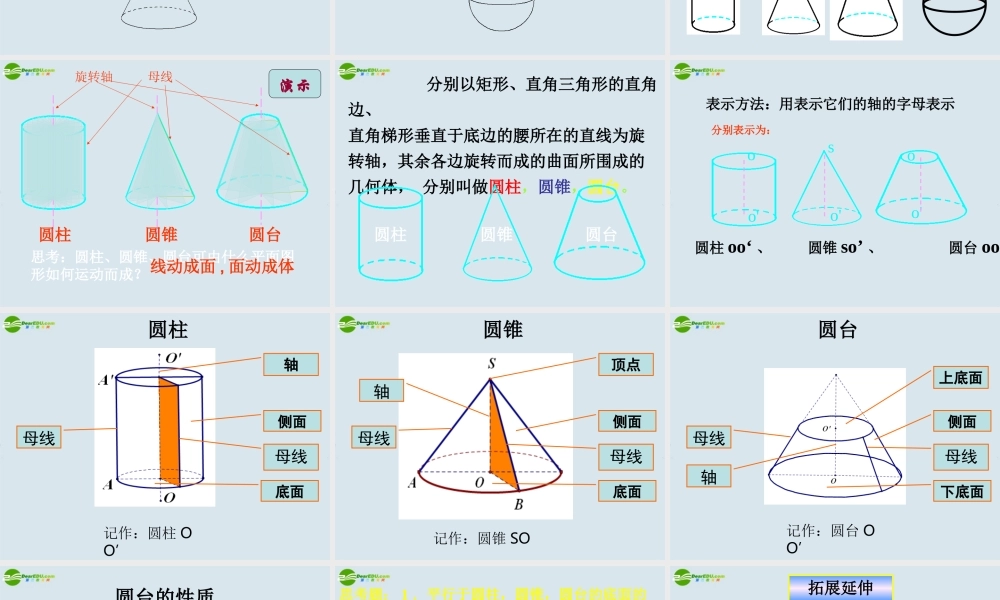
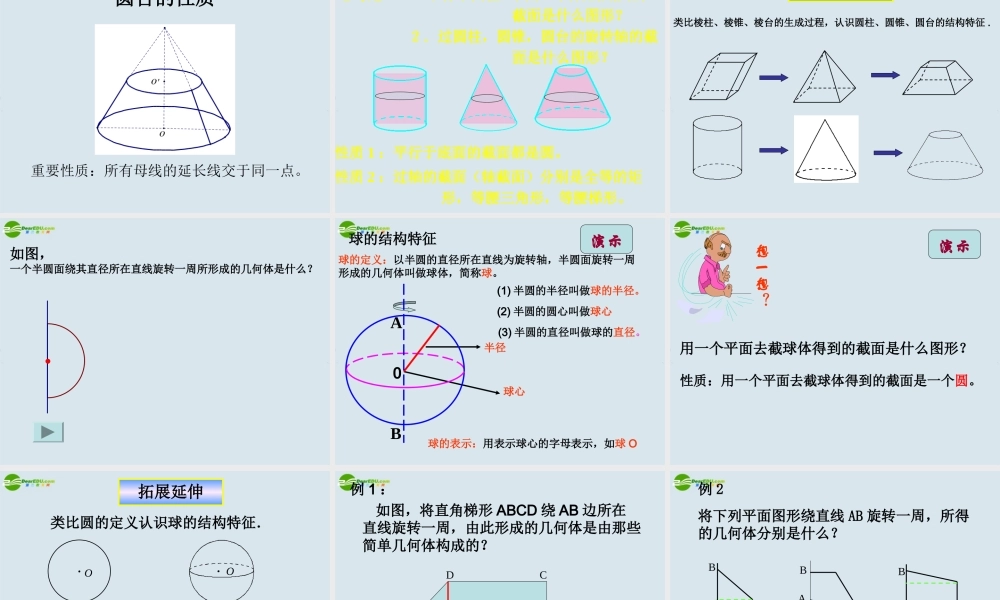
情境引入情境引入情境引入情境引入情境引入思考:这个几何体的外部曲面是如何形成的? 几何体是如何形成的?下面几何体与多面体不同 , 仔细观察下列几何体 , 它们有什么共同点或生成规律 ?圆锥圆柱圆台思考:圆柱、圆锥、圆台可由什么平面图形如何运动而成?线动成面 , 面动成体 母线旋转轴演示 分别以矩形、直角三角形的直角边、直角梯形垂直于底边的腰所在的直线为旋转轴,其余各边旋转而成的曲面所围成的几何体, 分别叫做圆柱,圆锥,圆台。圆柱圆锥圆台表示方法:用表示它们的轴的字母表示oo'o'soo' 圆柱 oo‘ 、 圆锥 so’ 、 圆台 oo' 分别表示为:圆柱侧面轴母线底面记作:圆柱 OO’母线圆锥侧面顶点母线底面记作:圆锥 SO母线轴圆台侧面上底面母线下底面记作:圆台 OO’母线轴圆台的性质重要性质:所有母线的延长线交于同一点。思考题: 1 .平行于圆柱,圆锥,圆台的底面的 截面是什么图形? 2.过圆柱,圆锥,圆台的旋转轴的截 面是什么图形?性质 1 :平行于底面的截面都是圆。性质 2 :过轴的截面(轴截面)分别是全等的矩 形,等腰三角形,等腰梯形。拓展延伸类比棱柱、棱锥、棱台的生成过程,认识圆柱、圆锥、圆台的结构特征 .如图,一个半圆面绕其直径所在直线旋转一周所形成的几何体是什么? 球的结构特征球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体叫做球体,简称球。(1) 半圆的半径叫做球的半径。(2) 半圆的圆心叫做球心(3) 半圆的直径叫做球的直径。球的表示:用表示球心的字母表示,如球 O球心半径OAB演示用一个平面去截球体得到的截面是什么图形? 性质:用一个平面去截球体得到的截面是一个圆。想一想?演示拓展延伸类比圆的定义认识球的结构特征.OO圆 :球 :和一个定点距离等于定长的点的集合.和一个定点距离等于定长的点的集合.平面内空间中例 1 : 如图,将直角梯形 ABCD 绕 AB 边所在 直线旋转一周,由此形成的几何体是由那些简单几何体构成的?ABCDAB图 1AB图 2AB图 3例 2 将下列平面图形绕直线 AB 旋转一周,所得的几何体分别是什么?演示课堂练习1. 一个直角三角形绕它的斜边边旋转一周形成的空间几何体是( ) A .一个圆锥 B .一个圆锥和一个圆柱 C .两个圆锥 D .一个圆锥和一个圆台2. 下列说法错误的是( ) A .圆柱的所有母线互相平行 B .圆锥的所有母线相交于一点C .圆台的所有母线延长后相交于...