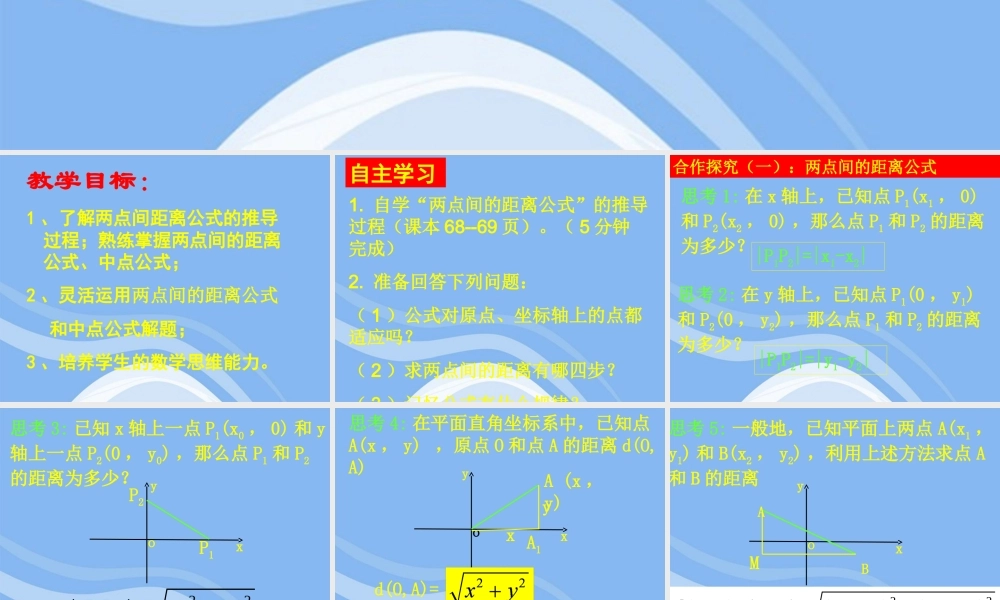
教学目标:1 、了解两点间距离公式的推导过程;熟练掌握两点间的距离公式、中点公式;2 、灵活运用两点间的距离公式 和中点公式解题;3 、培养学生的数学思维能力。自主学习1. 自学“两点间的距离公式”的推导过程(课本 68--69 页)。( 5 分钟完成)2. 准备回答下列问题:( 1 )公式对原点、坐标轴上的点都适应吗?( 2 )求两点间的距离有哪四步?( 3 )记忆公式有什么规律? 合作探究(一):两点间的距离公式思考 1: 在 x 轴上,已知点 P1(x1 , 0)和 P2(x2 , 0) ,那么点 P1 和 P2 的距离为多少? 思考 2: 在 y 轴上,已知点 P1(0 , y1)和 P2(0 , y2) ,那么点 P1 和 P2 的距离为多少? |P1P2|=|x1-x2||P1P2|=|y1-y2|思考 3: 已知 x 轴上一点 P1(x0 , 0) 和 y轴上一点 P2(0 , y0) ,那么点 P1 和 P2的距离为多少? 221200||PPxyxyoP1P2思考 4: 在平面直角坐标系中,已知点A(x , y) ,原点 O 和点 A 的距离 d(O,A)xyoA1A (x ,y)yxd(O,A)= 思考 5: 一般地,已知平面上两点 A(x1 ,y1) 和 B(x2 , y2) ,利用上述方法求点 A和 B 的距离222121( ,) ||()()d A BABxxyyxyoBAM)()(1212),(22yyxxABBAd1 、公式: A ( x1,y1 )、 B(x2,y2) 两点间的距离,用 d ( A , B )表示为由特殊得到一般的结论【例 1 】已知 A ( 2 、 -4 )、 B ( -2 ,3 ) . 求 d ( A , B )6574)(B)d(A,22〖课堂检测 1 〗课本第 71 页练习 A , 1. 求两点间的距离。题型分类举例与练习【例 2 】已知:点 A(1 , 2) , B(3 , 4) ,C(5 , 0) 求证:三角形 ABC 是等腰三角形。证明:因为 d(A,B)=d(A,C)= d(C,B)=即 |AC|=|BC| 且三点不共线所以,三角形 ABC 为等腰三角形。〖课堂检测 2 〗 已知: A ( 1 , 1 ) B( 5 , 3 ) C ( 0 , 3 )求证:三角形 ABC是直角三角形225252 【例 3 】证明平行四边形四条边的平方和等于两条对角线的平方和的两倍 .xyA(0,0)B(a,0)C (b, c)D (b-a, c)该题用的方法 ---- 坐标法。可以将几何问题转化为代数问题。记住结论。 用“坐标法”解决有关几何问题的基本步骤:第一步;建立坐标系,用坐标表示有关的量第二步:进行有关代数运算第三步:把代数运算结果“ 翻译”成几何关系 2 、...