高中数学 215平面上两点间的距离课件 苏教版必修2 课件VIP免费

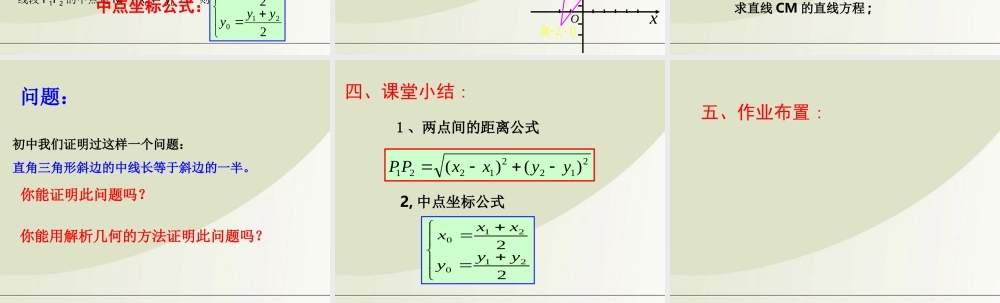
平面上两点间的距离一、复习引入 :试求：两点间的距离已知： 和 ，111yxP，222yxP，xoy1 ）、 y1=y21x2x2 ）、 x1=x2xoy1y2y||1221xxPP||1221yyPP111yxP，222yxP，111yxP，222yxP，二、构建数学 :xoy21yxQ，2121,)3yyxx、21221221)()(yyxxPP两点 间的距离111yxP，222yxP，111yxP，222yxP，练习 : （ 1 ）两点 的距离是 ________ ． )5,2(,31BA，（ 2 ）两点 的距离是 17 ，则 a=______ ．)5,(,100aBA ，13±8已知 B （ -2-1 ）， C （ 4 ， 7 ），如何求 BC 中点坐标？)1,2(B)7,4(C),(yxM),4(1yC)1,(1xB一般地，对于平面上的两点 P1 （ x1 ， y1 ）， P2 （ x2 ， y2 ），线段 P1P2 的中点是 M （ x0 ， y0 ），则 ：22210210yyyxxx中点坐标公式：)1,4( N三、数学应用 :例 1 已知 的顶点坐标为 A(-1 ， 5) ， B(-2 ， -1) ， C(4 ， 7) （ 1 ）求 BC 边的长 ； （ 2 ）求 BC 边上的中线 AM 的长； （ 3 ）求 BC 边上的中线 AM 所在直线的方程。ABCOxy( 2, 1)B (4,7)C( 1,5)A M练习 : （ 2 ）已知 的顶点坐标为 A （ 3 ， 2 ）， B （ 1 ，0 ）， ， 求 AB 边上的中线 CM 的长； 求直线 CM 的直线方程 ;)31,32(CABC(1) 求线段 AB 的长及其中点坐标 ①A(8,10) , B(-4,4) ②)3,2(),2,3(BA问题：初中我们证明过这样一个问题：直角三角形斜边的中线长等于斜边的一半。你能证明此问题吗？你能用解析几何的方法证明此问题吗？21221221)()(yyxxPP1 、两点间的距离公式2, 中点坐标公式22210210yyyxxx四、课堂小结 :五、作业布置 :